Homework 6

Directions:

  1. Show each step of your work and fully simplify each expression.
  2. Turn in your answers in class on a physical piece of paper.
  3. Staple multiple sheets together.
  4. Feel free to use Desmos for graphing.

Answer the following:

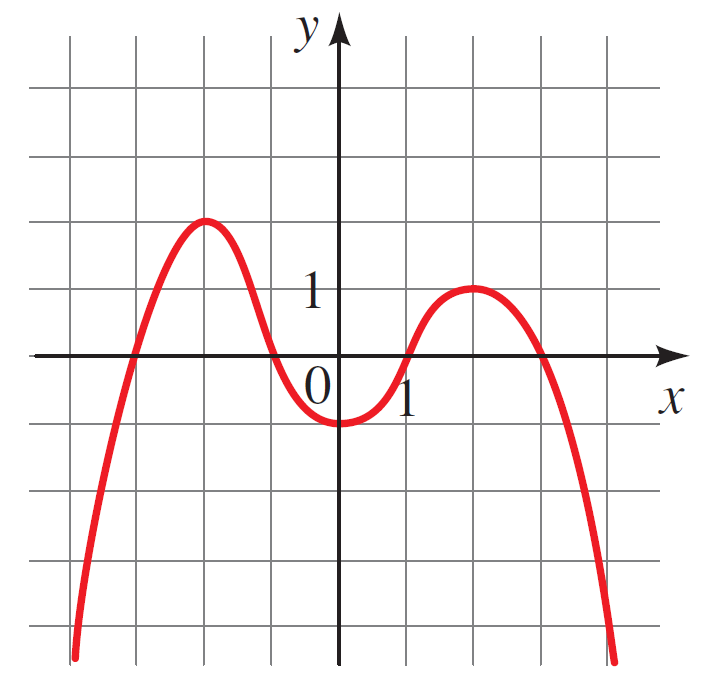
  1. Given the two functions $f$ and $g$
    1. Solve the equation $f(x) = g(x)$.
    2. Solve the equation $f(x) < g(x)$.
    3. Solve the equation $f(x) \geq g(x)$.
    4. On what intervals is $f(x)$ increasing and decreasing?
    5. On what intervals is $g(x)$ increasing and decreasing?
    6. What is the local maxima of $f(x)$?
  2. Solve the following equations/inequalities with 1.5 methods or using the graph. You can use Desmos (but graph both graphs on the homework you will submit).
    1. $x - 2 = 4 - x$
    2. $x^3 + 3x^2 = -x^2 + 5x$
    3. $x^3 + 3x^2 < -x^2 + 5x$
    4. $16x^3 + 16x^2 = x + 1$
    5. $1 + \sqrt{x} = \sqrt{x^2 + 1}$
  3. Find the increasing/decreasing intervals and all local maxima/minima and the location at which they occur:
  4. What is the average rate of change of $f(x)$ on $(x, x + h)$ defined as?
  5. If a function has negative average rate of change on $(a, b)$, must it be decreasing on $(a, b)$? If not, draw a counterexample.
  6. Find the average rate of change for the following functions between the given values. Fully simplify when necessary.
    1. $f(x) = \sqrt{x}; \qquad (x, x + h)$
      Hint Rationalize the numerator.
    2. $f(x) = x^3 - 4x^2; \qquad (0, 10)$
    3. $f(x) = 3x - 2; \qquad (2, 3)$
    4. $f(x) = 1 - 3x^2; \qquad (2, 2 + h)$
    5. $f(x) = \dfrac{1}{x}; \qquad (x, x + h)$
  7. Which transformations should be last?
  8. If I have a base function $f(x)$, explain in English what the following transformations will do to $f(x)$:
    1. $f(x + 2)$
    2. $f(-x)$
    3. $-f(x) - 3$
    4. $-f(-2x + 4)$
    5. $3-f\left(-\frac{1}{2}x + 2\right)$
  9. Suppose \[f(x) = \sqrt{x} \qquad g(x) = \sqrt{-x - 2} \qquad h(x) = \sqrt{- x + 2} \qquad i(x) = \sqrt{-(x + 2)}\]
    1. Is $g(x)$ horizontally shifted two units to the right from $f(x)$? Why or why not?
    2. Is $h(x)$ horizontally shifted two units to the right from $f(x)$? Why or why not?
    3. Is $i(x)$ horizontally shifted two units to the right from $f(x)$? Why or why not?
  10. Suppose \[f(x) = x^3 \qquad g(x) = \left(-x - 4\right)^3 \qquad h(x) = \left(-x + 4\right)^3 \qquad i(x) = (-(x+4))^3\]
    1. Is $g(x)$ horizontally shifted four units to the left from $f(x)$? Why or why not?
    2. Is $h(x)$ horizontally shifted four units to the left from $f(x)$? Why or why not?
    3. Is $i(x)$ horizontally shifted four units to the left from $f(x)$? Why or why not?
  11. Write out the list of transformations in the order needed to transform the parent function into $f(x)$.
    1. $f(x) = \sqrt{x + 4} - 3$
      Hint Parent is $g(x) = \sqrt{x}$
    2. $f(x) = 2-(x-1)^2$
      Hint Parent is $g(x) = x^2$
    3. $f(x) = 4 - \sqrt{-2x + 4}$
      Hint Parent is $g(x) = \sqrt{x}$. Don't forget to factor out $-2$.
    4. $f(x) = -2\lvert{-x - 1}\rvert + 3$
      Hint Parent is $g(x) = \lvert x \rvert$. Don't forget to factor out $-1$.
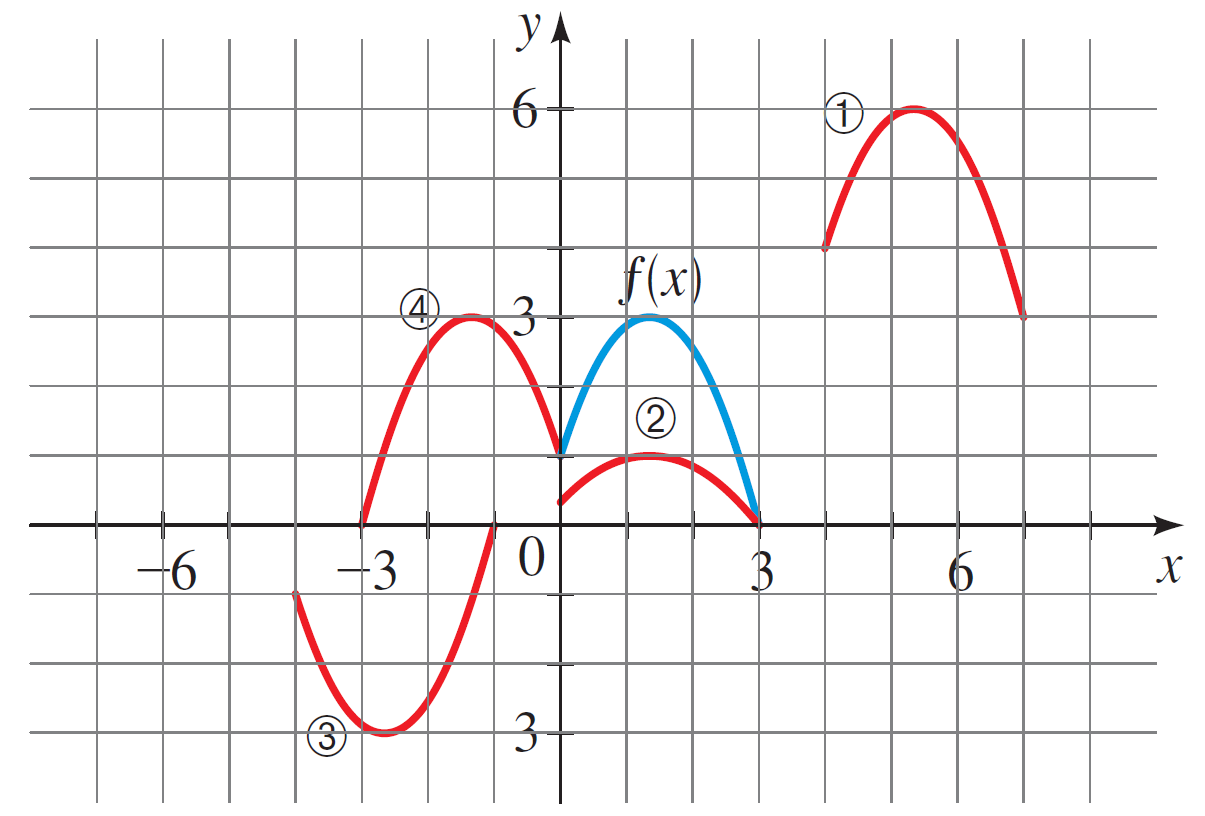
  12. For each red function, write out what the transformation from $f(x)$ should be:
  13. Graph the following functions using transformations. Include at least two transformed points and ordered of transformations you apply them in for full credit.
    1. $g(x) = \sqrt{x + 4} - 3$
    2. $g(x) = -(x-1)^2$
    3. $g(x) = -2 - \sqrt{-2x + 6}$
    4. $g(x) = -\lvert-2x - 2\rvert + 4$
    5. $g(x) = 2(-2x+6)^2 - 1$
  14. Suppose \[f(x) = 2x^2 + x \qquad g(x) = x^2 - x \qquad h(x) = x^2 - 1 \qquad k(x) = x^4\] Evaluate and expand the following:
    1. $f(x) + g(x) + h(x)$
    2. $f(x) - g(x)$
      Hint Look at how many terms you are substituting. Don't forget...
    3. $g(x)h(x) - k(x)$
    4. $f(x)\left[k(x)\right]^2$
    5. $\dfrac{g(x)}{h(x)}$ (also find the domain).
  15. Consider $f(x) = x^2 -1$ and $g(x) = x^2 + 2x + 1$. We make a new function $h(x) = \dfrac{g(x)}{f(x)}$.
    1. Find and simplify the formula for $h(x)$.
    2. What are the $x$-values of the holes in $h(x)$?
    3. What is the domain of $h(x)$?
  16. Suppose \begin{align}f(x) &= (x^2 - 1)^3 \\ f'(x) &= 6x(x^2 - 1)^2 \\ g(x) &= x^2 + 1 \\ g'(x) &= 2x\end{align} Evaluate and simplify the following:
    1. $\dfrac{g'(x)f(x) - f'(x)g(x)}{\left[g(x)\right]^2}$
      Hint Look at how many terms you are substituting. Don't forget...
    2. $f'(x)g(x) + f(x)g'(x)$
  17. Given the functions $f(x) = 2x- 5$ and $g(x) = 3 - x^2$, evaluate the following and fully simplify.
    Hint Expand because like terms are created.
    1. $f\circ g$
    2. $f(g(0))$
    3. $g \circ f$
    4. $f \circ f$
    5. $g \circ g$
    6. $f \circ f \circ f$
  18. Given the following functions $F(x)$, find two functions $f$ and $g$ where $f\circ g = F$.
    Choosing $f(x) = x$ or $g(x) = x$ is zero credit for this problem.
    1. $F(x) = (x-3)^4$
    2. $F(x) = (2x-3)^{-\frac{1}{2}}$
    3. $F(x) = \sqrt{1 - \sqrt{x}}$
    4. $F(x) = \sqrt{(x^2 + 2x + 3)^3}$