Homework 9

Directions:

Show each step of your work and fully simplify each expression.
Turn in your answers in class on a physical piece of paper.
Staple multiple sheets together.
Feel free to use Desmos for graphing.

Answer the following:

Suppose a polynomial $P(x)$ has real coefficients. If $P(x)$ factors as $(x - i)Q(x)$, what other factor must be present in $P(x)$?
Find a degree 4 polynomial with zeros $-2i$ and $1 - i$.
Find a degree 6 polynomial with zeros $3, -2, i$ and $\dfrac{1 - i\sqrt{3}}{2}$.
True or False: it is possible for a polynomial $P(x)$ with real coefficients to factor like \[P(x) = (x-2)(2x - 3i)(x+2)\]
If $y \rightarrow -\infty$ as $x \rightarrow 2^+$, what is the line $x = 2$ called?
If $y \rightarrow 3$ as $x \rightarrow -\infty$, what is the line $y = 3$ called?
Find the vertical and horizontal asymptotes for the following rational functions, if any. If the rational function has a hole, make sure to redefine it in it's simpler form (the domain restriction).
1. $f(x) = \dfrac{4x - 4}{x + 2}$
2. $f(x) = \dfrac{(x+1)(2x-3)}{(x-2)(4x+7)}$
3. $f(x) = \dfrac{3x + 1}{4x^2 + 1}$
4. $r(x) = \dfrac{x^2 - 1}{x^2 + 2x + 1}$
5. $f(x) = \dfrac{4x^2 - 1}{2x^2 + 7x + 3}$
6. $f(x) = \dfrac{x^3 - x^2}{x^2 - 3x - 2}$
What horizontal and vertical asymptotes does this graph have?
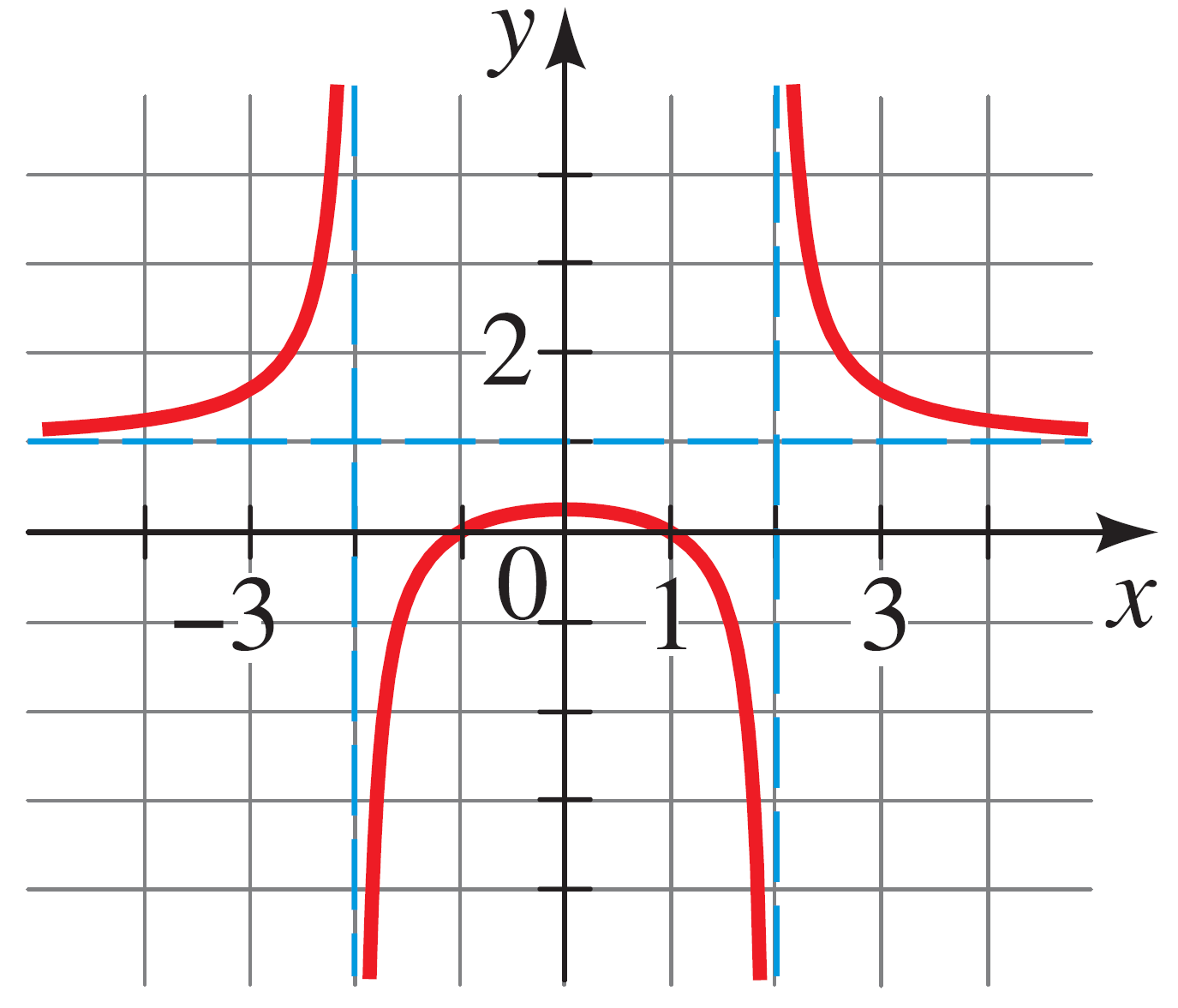
The rational function \[r(x) = \dfrac{x^3 - 5x^2 + 3x + 9}{x+1}\] has a hole at $x = -1$.
1. What factor must be present in the numerator?
2. Use the division algorithm to divide the numerator and sketch a rough graph.
  Hint You will get a quadratic, put in standard form $a(x-h)^2 + k$.
Given the function $f(x) = 4^x$, evaluate:
1. $f(1)$
2. $f\left(\dfrac{1}{2}\right)$
3. $f(2)$
4. $f\left(\dfrac{3}{2}\right)$
Hint Your answers will be numbers, no exponents.
Suppose $f(x) = a^x$ where $a > 0, a \neq 1$.
1. What asymptotes does $f(x)$ have?
2. What's the domain and range of $f(x)$?
If $f(x) = 2^x$, evaluate and simplify the expression \[\dfrac{f(x + h) - f(x)}{h}\] so there is one fraction with $h$'s in it.
Hint $2^{x+h} = 2^x \cdot 2^h$ by LoE.
You found a bank which doubles your deposited money every day 🤯.
You deposit one penny at day $t = 0$. The next day ($t = 1$) you have two pennies, and the second day you have four pennies.
1. Find an exponential function $f(t)$ which can describe the amount of money you have after $t$ days.
2. How many days does it take for your balance to surpass one million dollars? Desmos can help here.
3. What is your reaction to the answer from the previous part?
What is the difference between simple interest, compound interest, and APY?
If \$10,000 is invested at an interest rate of 3% per year, compounded semiannually, find the value of the investment after 5, 10, and 15 years.
Find the APY for an investment that earns 8% per year, compounded monthly.
You decide to open a Certificate of Deposit for one year, where your APY interest is credited monthly into your other savings account. Your principal is \$20,000 USD and the bank says the APY is 5%. Every month you receive around \$83.34. Is the bank properly paying out the APY of 5%?
Hint This is not a compound interest problem. Instead, the gain from APY is spread out each month.
Sketch a rough graph of the following functions using transformations: \[f(x) = 2^{-x} \qquad \qquad g(x) = -2^{x} \qquad \qquad h(x) = -2^{-x}\]
With a base function $f(x) = e^x$, state the order of transformations (and their numbers) the following functions use:
1. $g(x) = 1 + e^x$
2. $h(x) = e^{2x}$
3. $r(x) = 2 - e^{x-3}$
4. $g(x) = 4 + e^{3(x+2)}$
To obtain a larger financial gain, determine which interest rate is better after 50 years:
1. $5.125\%$ per year, compounded semiannually
2. $5\%$ per year, compounded continuously
Hint You don't need to set the principal to a number, just like what we did in class!
A drug was taken by an individual. The number of milligrams remaining in the person's bloodstream after $t$ hours is \[D(t) = 50e^{-t}\]
1. As $t \rightarrow \infty$, what does $D(t)$ approach? Do you think this behavior is appropriate to model our intuition from the real world?
2. How many milligrams of the drug remains in the bloodstream after 5 hours?
Animal populations are not capable of unrestricted growth because of limited habitat and food supplies. Under such conditions the population follows a logistic growth model: \[P(t) = \dfrac{d}{1 + ke^{-ct}}\] where $c,d$ and $k$ are positive constants. For a certain fish population in a small pond, we estimate $d = 1200, k = 11, c = 0.2$ and let $t$ be measured in years. The fish were introduced into the pond at time $t = 0$.
1. How many fish were originally put into the pond?
2. Find the fish population after 10, 20 and 30 years.
3. Evaluate $P(t)$ for large values of $t$. In fact, as $t\rightarrow \infty$, what does the population approach?
4. From your answer in part $(c)$, what does the constant $d$ represent?
5. Graph $P(t)$ in Desmos. Does this function make sense in terms of a limited habitat and food supplies?
6. From part $(d)$, what does this show us about setting parameters in functions? If this was a real life scenario, could we use these same ideas to model real life phenomena?
Suppose $f(x) = \log_a x$ where $a > 0, a \neq 1$.
1. What asymptotes does $f(x)$ have?
2. What's the domain and range of $f(x)$?
Express the equation in exponential form:
1. $\log_35 = x$
2. $\log_381 = 4$
3. $\ln(x-1) = 4$
4. $\ln(x^2 - x - 2) = 3$
Evaluate the expression:
1. $\log_22$
2. $\log_636$
3. $\log_{10}\sqrt{10}$
4. $\log_{49}7$
5. $\log_77^{10}$
6. $\ln(1/e)$
7. $e^{\ln3}$
8. $\ln e^4$
9. $\log_51$
Use the definition of the logarithm to find the number $x$.
1. $\log_3 x = -2$
2. $\log_x16 = 4$
3. $\ln e^2 = x$
4. $\log_x6 = \dfrac{1}{2}$
5. $\ln x = -1$
Explain why $f(x) = \ln(x - 3)$ is horizontally shifted to the right three units from $g(x) = \ln x$.
Use transformations to sketch the following:
1. $f(x) = \ln(-x)$
2. $f(x) = - \ln(- x - 2)$

The rest of these problems will be on the last homework assigned next week. Skip for now.

State which of the following are true or false:
1. $\ln 3x = \ln 3 + \ln x$
2. $\ln(3 + x) = \ln 3 + \ln x$
3. $\ln\left[x(x-1)\right] = \ln x + \ln (x - 1)$
4. $\ln x^2 = 2\ln x$
5. $(\ln x)^2 = 2\ln x$
6. $\log_2(x - 3) = \log_2 x - \log_2 3$
7. $\ln\left(\dfrac{x}{x - 1}\right) = \ln x - \ln (x - 1)$
Use Laws of Logarithms to evaluate the expression without a calculator. Your answer will be one number.
1. $\log 5 + \log 20$
2. $\log_5 \sqrt{5}$
3. $\log_2 60 - \log_2 15$
4. $\log_4 16^{100}$
5. $\ln (\ln e^{e^{200}})$
Expand these logarithms using Laws of Logarithms:
1. $\log_3 4x^2$
2. $\ln \sqrt{x^2y}$
3. $\ln \dfrac{3x^2}{(x - 1)^4}$
4. $\ln \sqrt[3]{\dfrac{x-1}{b + 2}}$
5. $\log_7 x(x+1)^2$
6. $\ln(\ln(x)\ln(y))$