11.1: Parabolas

Motivation

Chapter 11 deals with conic sections. These are curves formed when a plane cuts a cone:

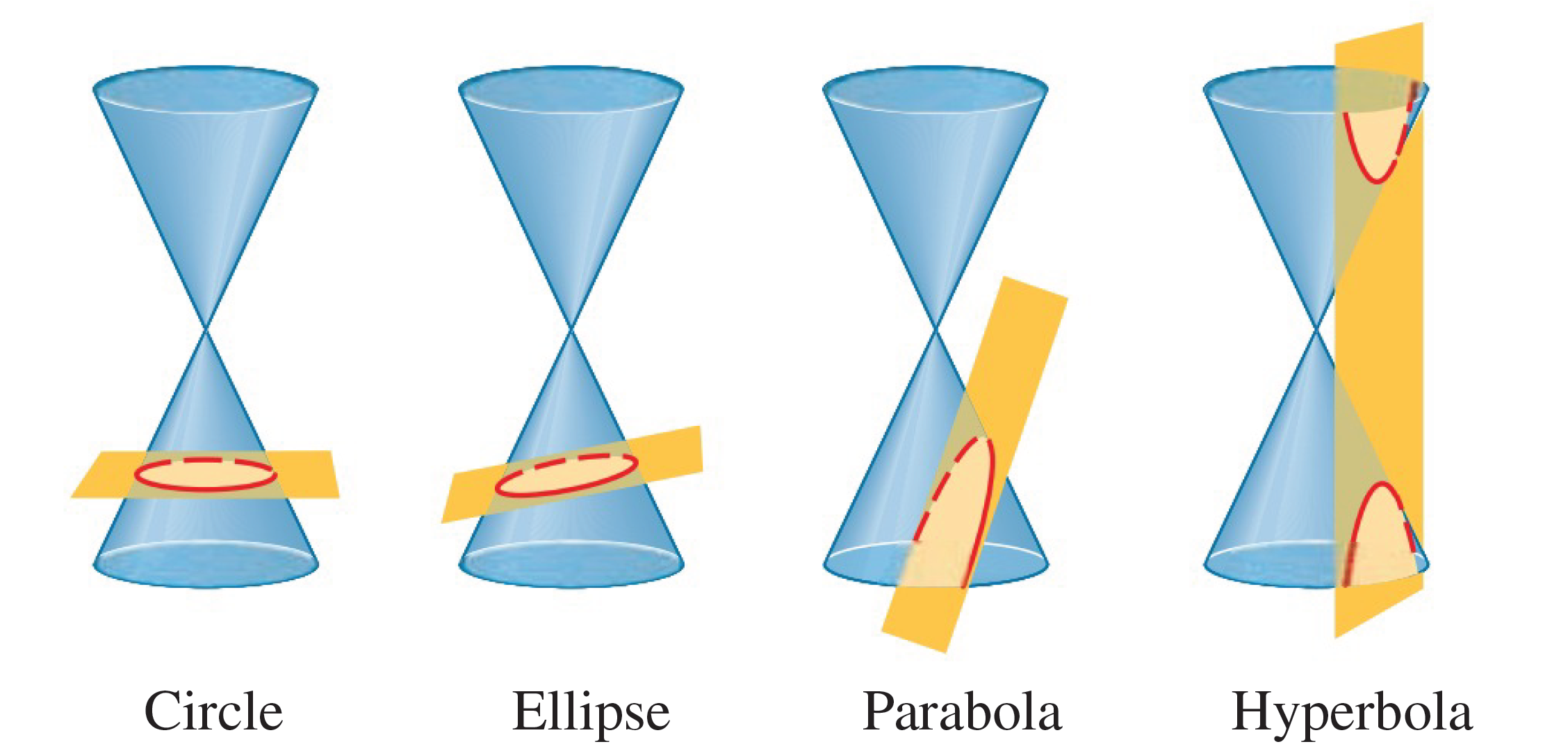
This section deals with parabolas.

Geometric Definition of a Parabola

We know about the algebraic formulation of a parabola; it's the quadratic equation: \[y = ax^2 + bx + c\]

There is also a geometric definition:

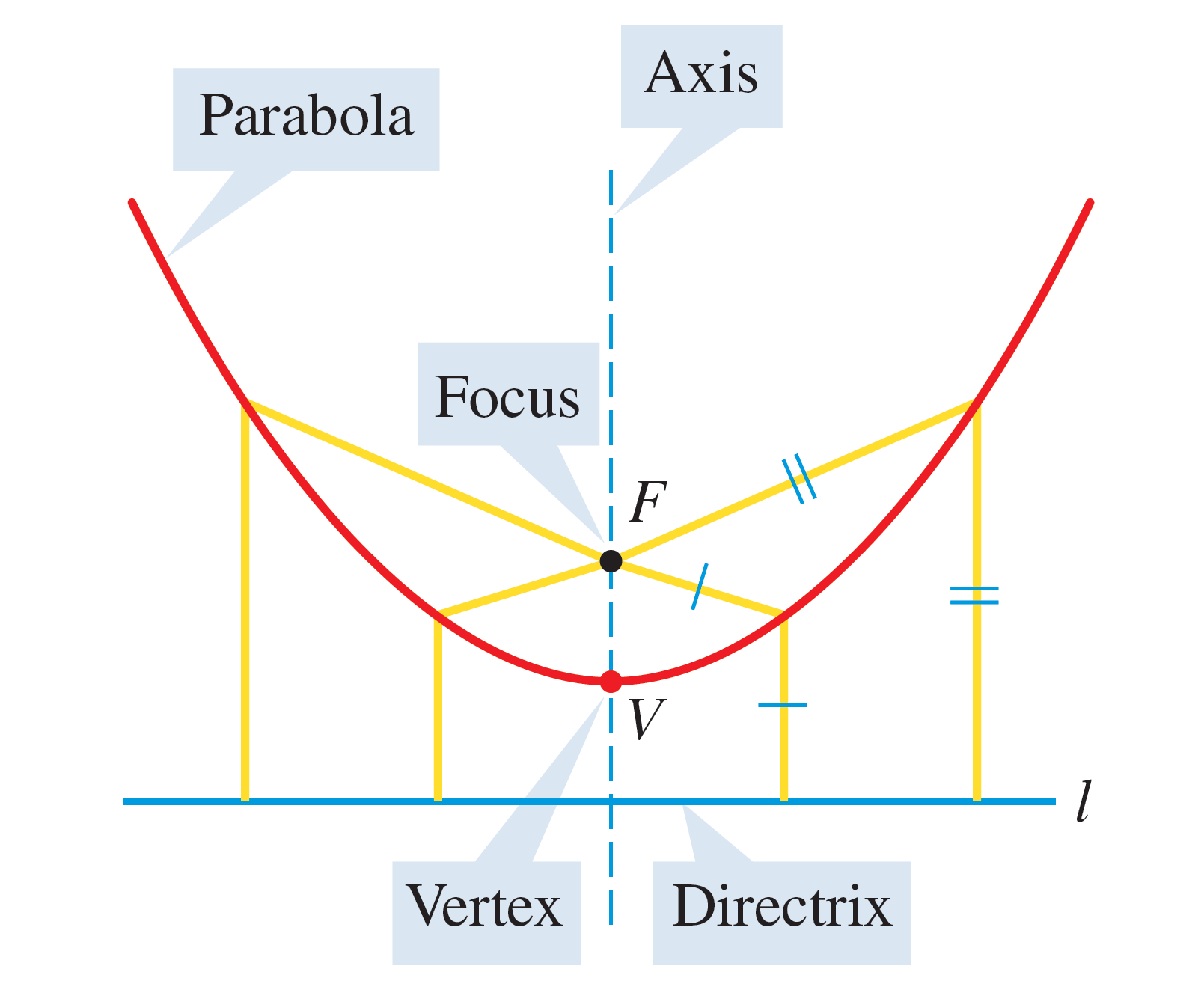
A parabola is the set of all points in the plane that are equidistant from a fixed point $F$ (called the focus) and a fixed line $\ell$ (called the directrix.)

Note that the focus is always in the direction the parabola opens, and the directrix is on the other side.

Parabola with Vertical Axis

The graph of the equation \[x^2 = 4py\] is a parabola with the following properties: This parabola opens upwards or downwards.
Find the focus and directrix of the parabola $y = -x^2$. Sketch the graph, including the focus and directrix.
Find an equation of a parabola with vertex $(0, 0)$ and focus $(0, 2)$. Sketch the graph.

Parabola with Horizontal Axis

The graph of the equation \[y^2 = 4px\] is a parabola with the following properties This parabola opens left or right.
A parabola has the equation $6x + y^2 = 0$. Find the focus and directrix of the parabola and sketch a graph.
For the following problems, find an equation of the parabola with vertex at the origin satisfying the following conditions or state it's impossible to.
  1. Focus at $(0, 6)$
  2. Focus on the positive $x$-axis, directrix $y = 2$

Applications of Parabolas

Parabolas have a useful property: if a light source is placed at the focus of a parabola, all light beams that bounce off the parabola will travel outwards parallel to each other:

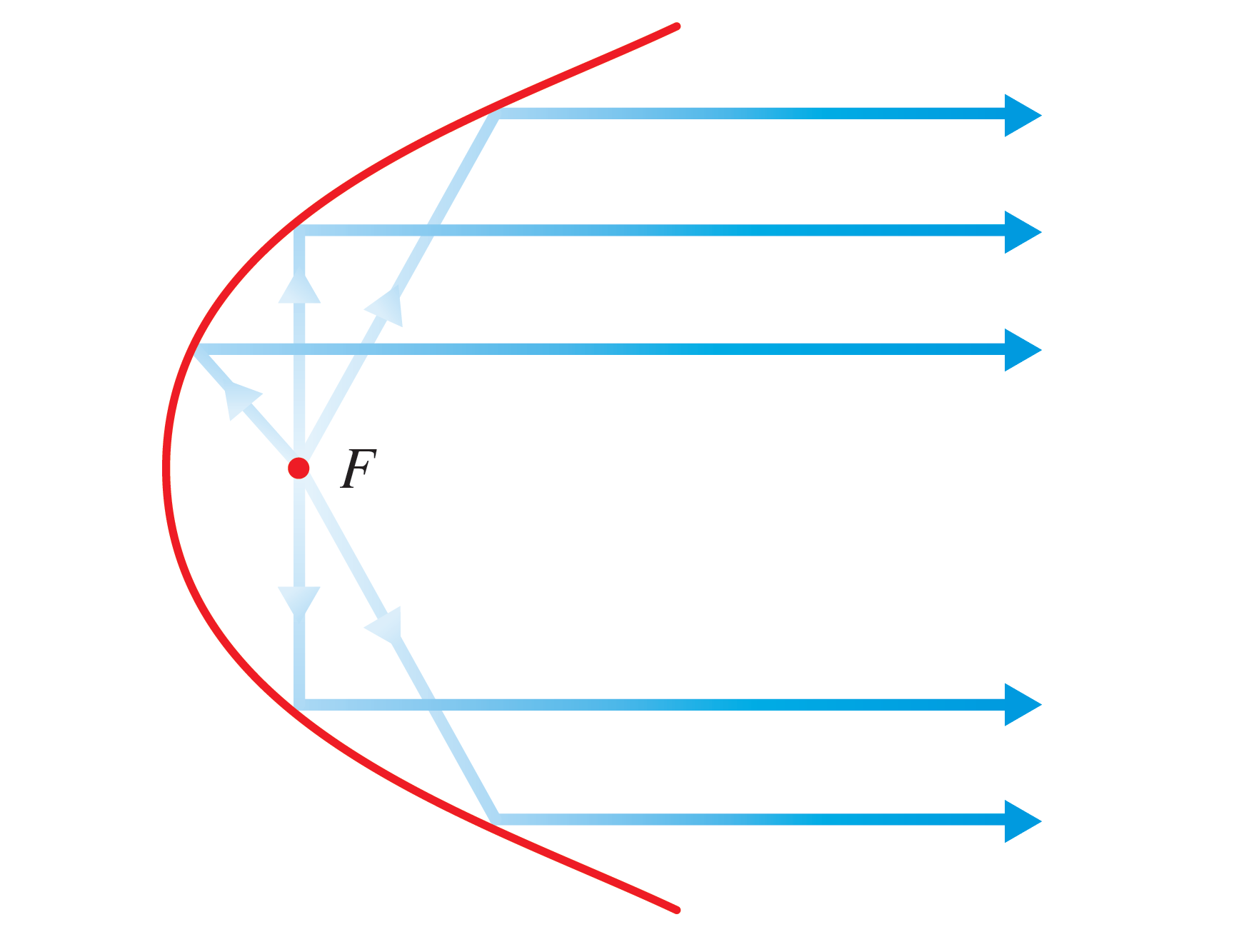
Thus parabolas are used in flashlights, automobile headlights, even satellite dishes! A signal from far away can bounce off the parabola back to the focus.

Another application is the trajectory of a projectile. When an object is thrown, neglecting air resistance, the path it creates is a parabola.