11.1: Ellipses

An ellipse is a curve that looks like an oval. Similar to the parabola, we have a geometric definition:

An ellipse is the set of all points where the sum of the distances from two fixed points $F_1$ and $F_2$ is a constant.
The two points $F_1$ and $F_2$ are the foci (plural of focus) of the ellipse.

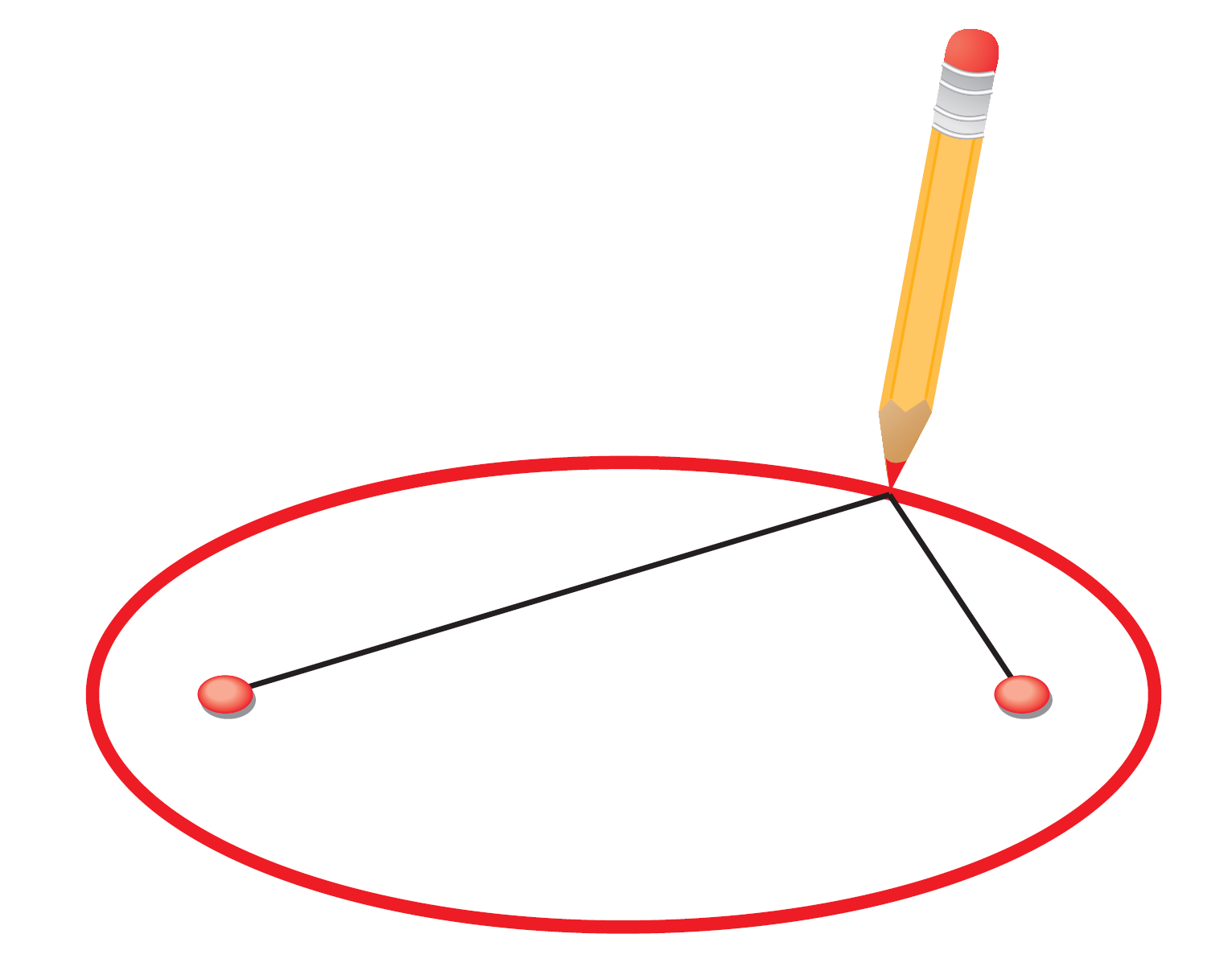
You can draw an ellipse by hand using the above technique. Nail a piece of string at its ends at two different points (these are the foci). Pull the string tight with a pencil, and perform one revolution.

This creates the set of all points where the sum of the distances from the foci is the same; the string length is the sum!

Equation and Graphs of Ellipses

The following equations are ellipses with center at the origin and the following properties:
An ellipse has the equation \[\dfrac{x^2}{9} + \dfrac{y^2}{4} = 1\]
  1. Find the foci, vertices, and lengths of the major/minor axes.
  2. Sketch a graph.
An ellipse has the equation \[16x^2 + 9y^2 = 144\]
  1. Find the foci, vertices, and lengths of the major/minor axes.
  2. Sketch a graph.
The vertices of an ellipse are $(\pm 4, 0)$ and the foci are $(\pm 2, 0)$. Find the equation.
Find the equation of the ellipse satisfying the following:
  1. Length of major axis is 4
  2. Length of minor axis is 2
  3. Foci on $y$-axis

Eccentricity of an Ellipse

What describes whether an ellipse is a skinny oval, or an almost round circle?

For the ellipses \[\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \qquad \qquad \dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1\] the eccentricity $e$ is the number \[e = \dfrac{c}{a}\] where $c = \sqrt{a^2 - b^2}$. Note that $0 < e < 1$.

The closer $e$ is to zero, the more circular the ellipse. The closer $e$ is to one, the more elongated the ellipse.

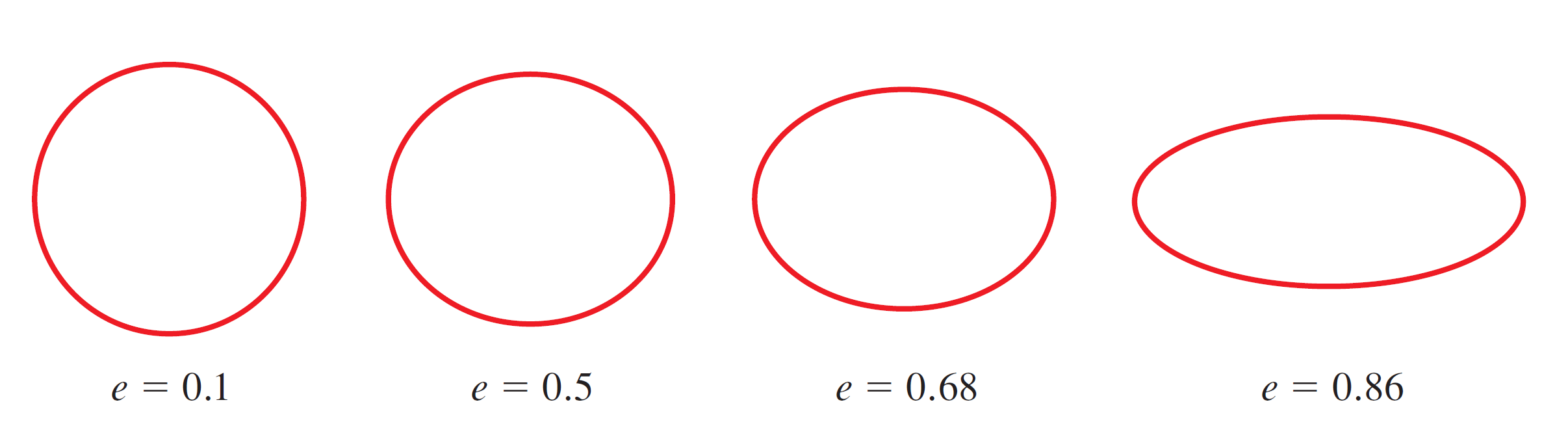
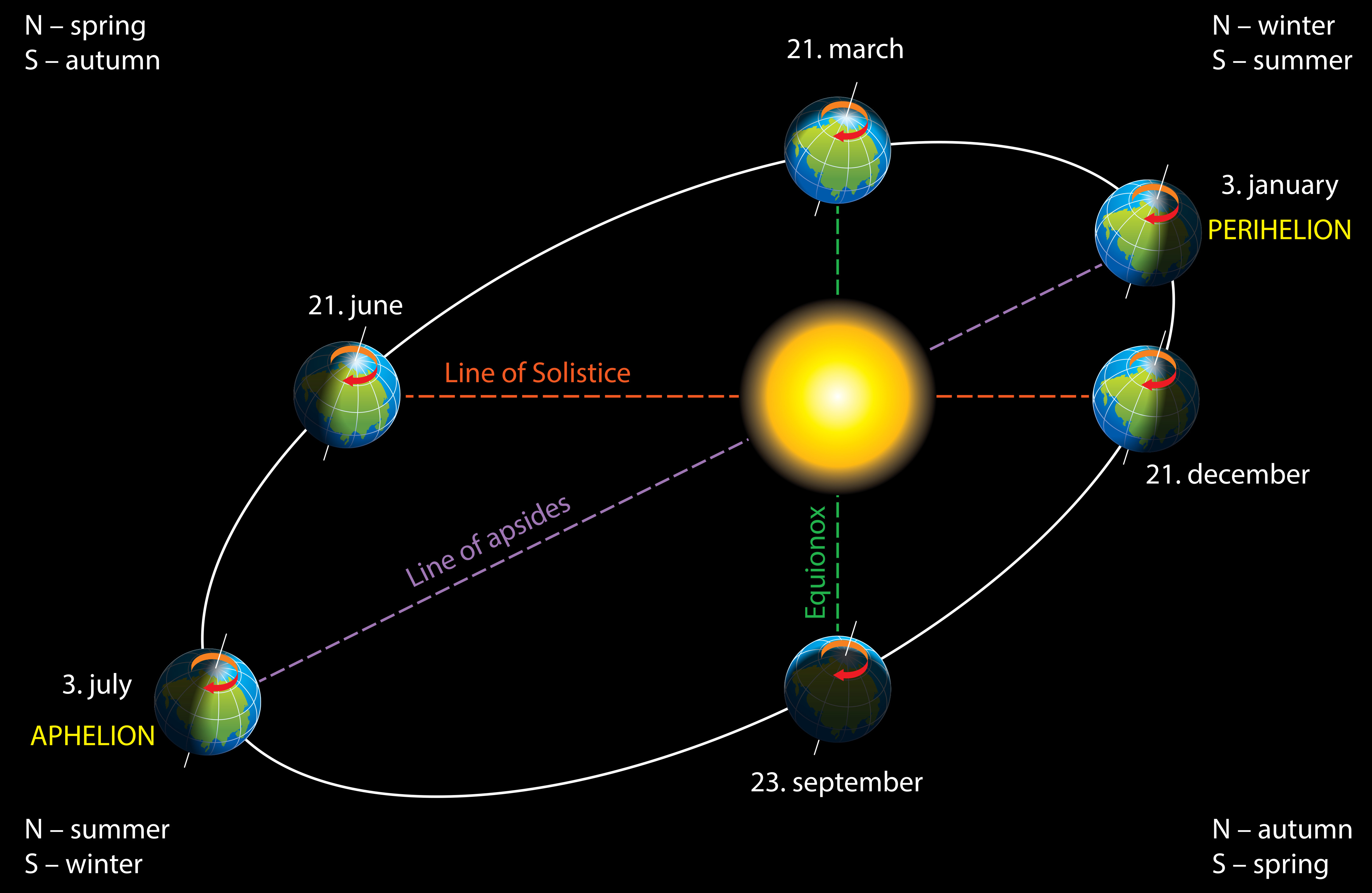
Find the equation of the ellipse with foci $(0, \pm 8)$, eccentricity $\dfrac{4}{5}$ and sketch the graph.

Applications of Ellipses

The orbits of planets are well-modelled by ellipses, including our Earth!

Other applications include elliptical exercise machines, or designing everyday objects in the shape of an ellipse.