11.3: Hyperbolas
The hyperbola is the last conic section we will study.
A hyperbola is the set of all points in the plane where the difference between two fixed points $F_1$ and $F_2$ is a constant.
The two points $F_1$ and $F_2$ are the foci of the hyperbola.
The two points $F_1$ and $F_2$ are the foci of the hyperbola.
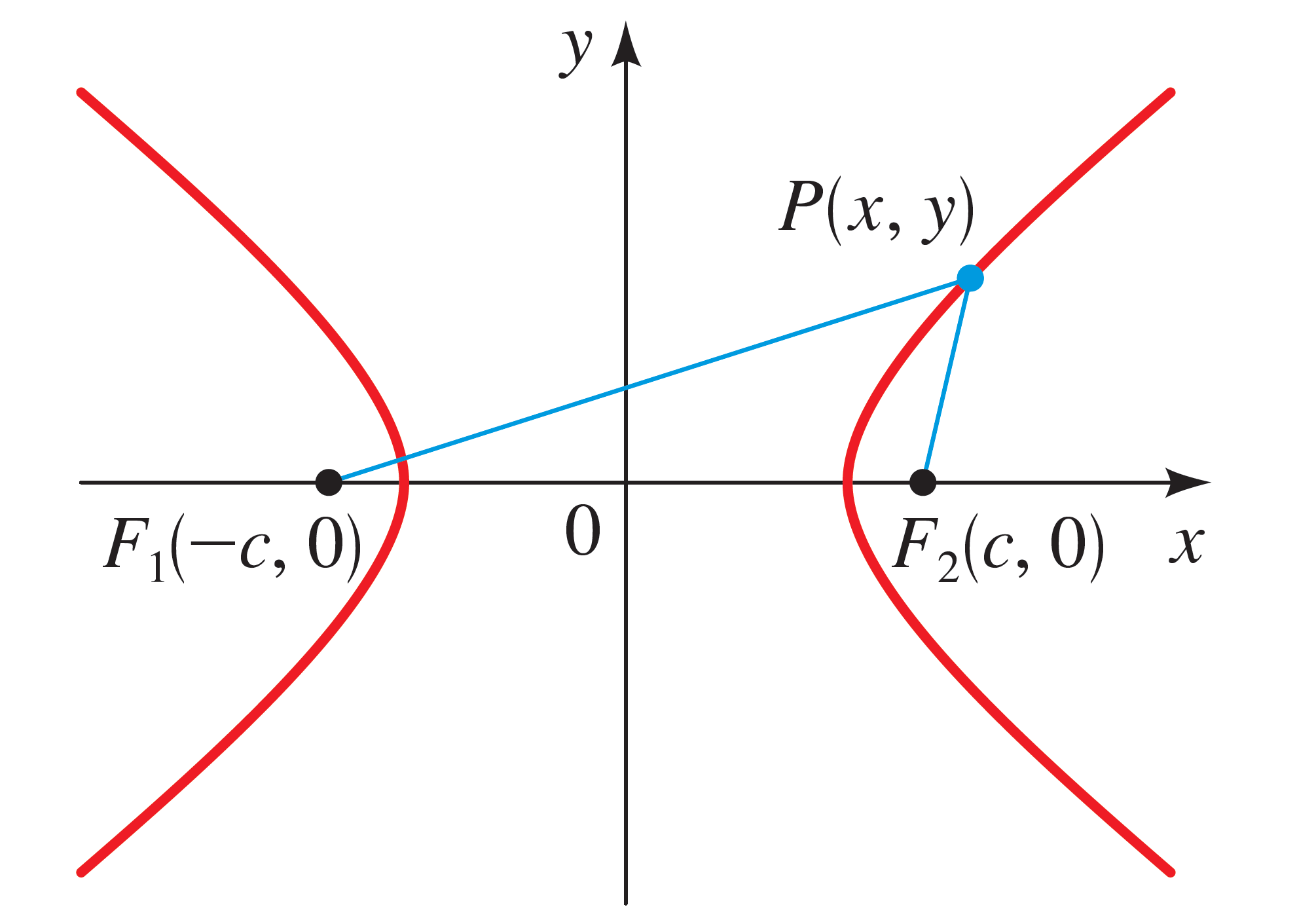
Equations and Graphs of Hyperbolas
The following equations are hyperbolas with center at the origin and the following properties:
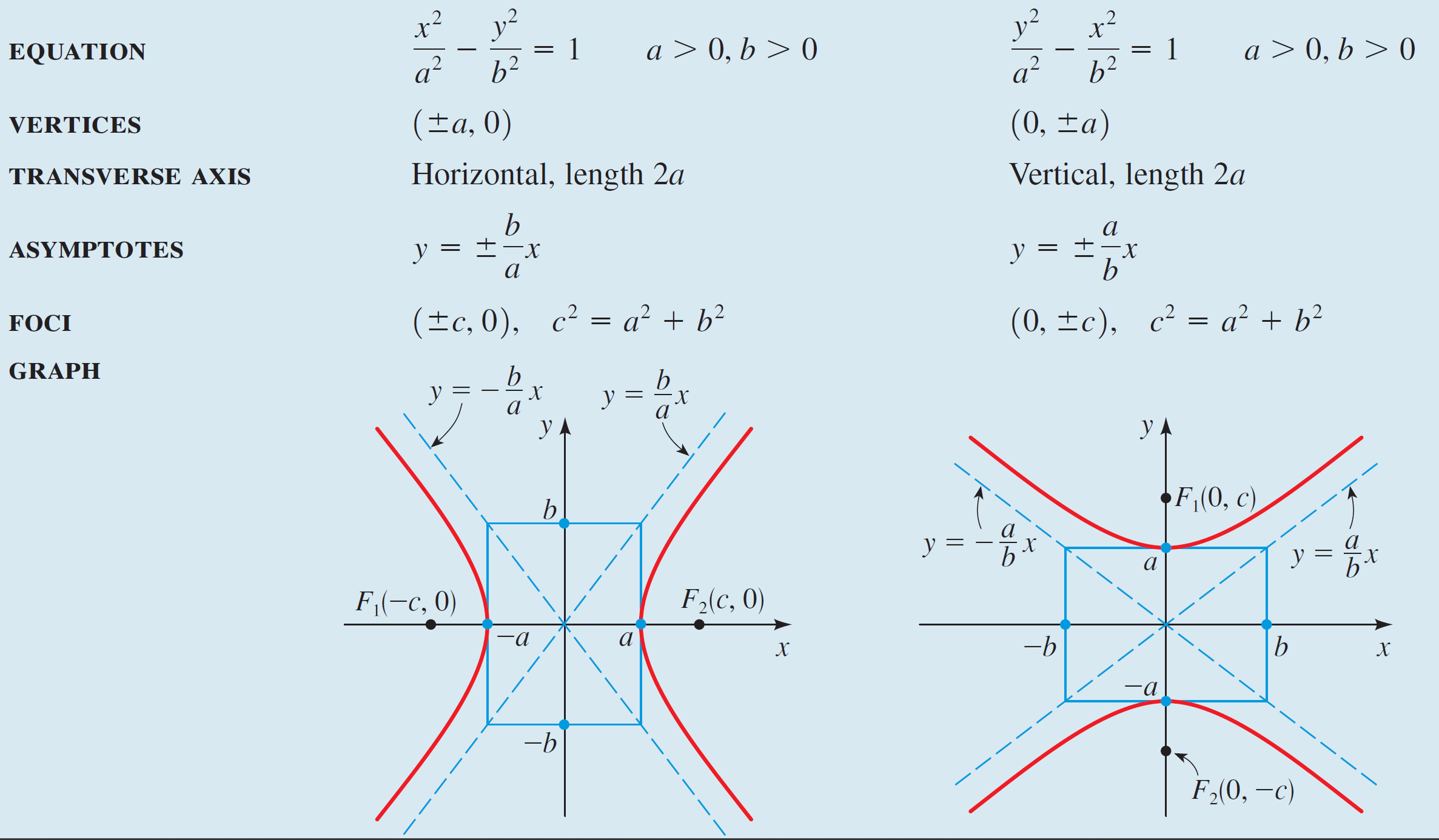

To sketch a hyperbola, first sketch the central box and the asymptotes. Then starting at the vertices, sketch each branch of the hyperbola approaching the asymptotes.
A hyperbola has the equation \[9x^2 - 16y^2 = 144\] Find the vertices, foci, length of the transverse axis, and asymptotes. Sketch a graph.
A hyperbola has the equation \[x^2 - 9y^2 + 9 = 0\] Find the vertices, foci, length of the transverse axis, and asymptotes. Sketch a graph.
A hyperbola has vertices $(\pm 3, 0)$ and foci $(\pm 4, 0)$. Find the equation of the hyperbola.
A hyperbola has vertices $(0, \pm 2)$ and asymptotes $y = \pm 2x$. Find the equation of the hyperbola.