8.1: Polar Coordinates

Motivation

Our coordinate system (called rectangular coordinates) involves $x$ (left-right movement) and $y$ (up-down movement).

Instead of $x$ and $y$, we can use distances and directions: start from the origin, and walk in the direction of the point.

Here's an animation comparing the two coordinate systems for the point $(2, 1)$.

Let's define the $r$ and $\theta$. Consider the following point $P$ in the coordinate plane:

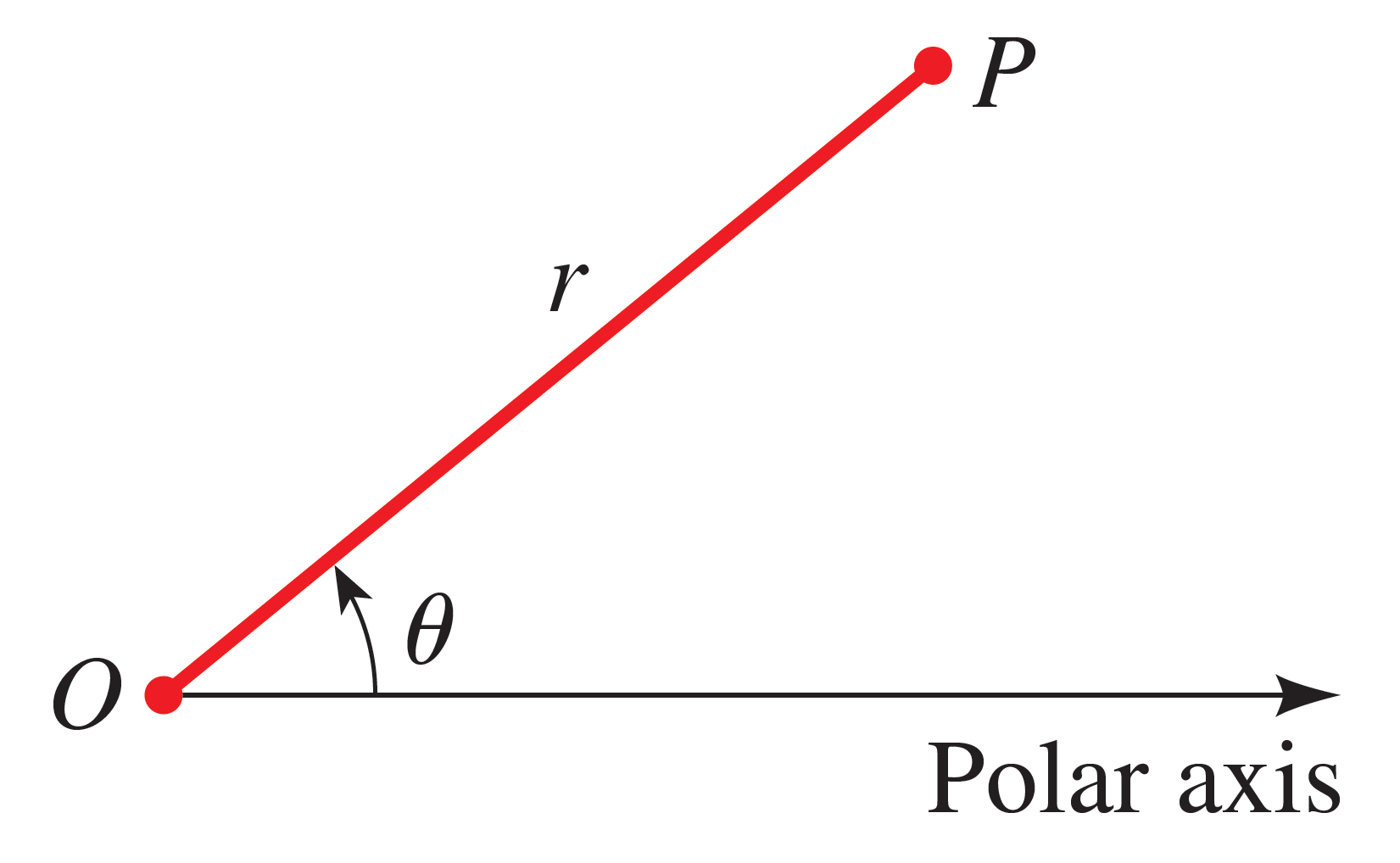
Point $O$ is usually anchored at the origin. The polar axis is then aligned along the positive $x$-axis.

Then:

  1. $r$ is the shortest distance from origin $O$ to $P$ (a straight line)
  2. $\theta$ is the angle between the polar axis and line segment $\overline{OP}$.

We already know if $\theta$ is positive, rotate counterclockwise. If $\theta$ is negative, rotate clockwise. For $r$:

  1. If $r$ is positive, then walk in the direction of $\theta$.
  2. If $r$ is negative, then walk in the opposite direction of $\theta$.

Finally, the new coordinate system is an ordered pair $(r, \theta)$.

Plot the following polar coordinates: \[\left(1, \dfrac{3\pi}{4}\right) \qquad \qquad \left(3, -\dfrac{\pi}{6}\right) \qquad \qquad\left(3, 3\pi\right) \qquad \qquad\left(-4, \dfrac{\pi}{4}\right)\]
Consider the polar coordinate $\left(2, \dfrac{\pi}{3}\right)$
  1. Graph it.
  2. Find two other polar coordinate representations with $r < 0$.

Relationship Between Polar and Rectangular Coordinates

How can we convert between $(r, \theta)$ and $(x, y)$? Here's a point with both coordinate systems labeled:

Note that $\cos \theta = \dfrac{x}{r}$.

Solving for $x$ gets $x = r\cos \theta$. The equation says plug in $r$ and $\theta$ to get $x$ out.

So we have:

To convert polar to rectangular coordinates, use \[x = r \cos \theta \qquad \qquad y = r \sin \theta\] To convert rectangular to polar coordinates, use \[r^2 = x^2 + y^2 \qquad \qquad \tan \theta = \dfrac{y}{x}, \quad x \neq 0\]
Convert $\left(4, \dfrac{2\pi}{3}\right)$ into rectangular coordinates.
Convert $\left(2, -2\right)$ into polar coordinates.

Careful: When converting rectangular to polar, $r^2 = x^2 + y^2$ will give you two $r$ values and tangent will respond with two different angles $\theta$.

Graph the point to determine which pairing of $(r, \theta)$ is appropriate.

Polar Equations

A polar equation is an equation involving only $r$ and $\theta$'s. For example \[r^3 = r \qquad \qquad r = \theta \qquad \qquad r = 1 - 2\sin \theta\] are all polar equations.

Convert $x^2 = 4y$ into polar coordinates.
Convert the following polar equations into rectangular form: \[r = 5\sec \theta \qquad \qquad r = 2\sin \theta \qquad \qquad r = 2 + 2\cos \theta\]