1.6: Calculating Limits Using the Limit Laws

The Limit Laws

We just saw two ways of computing limits: the table and the graph.

Both methods have their own weaknesses. We now turn to looking at algebraic manipulations.

Limit Laws
Suppose $c$ is a constant and the limits \[\lim_{x\rightarrow a}f(x), \qquad \lim_{x\rightarrow a} g(x)\] exist. Then:
  1. $\displaystyle\lim_{x\rightarrow a} [f(x) \pm g(x)] = \lim_{x\rightarrow a} f(x) \pm \lim_{x\rightarrow a} g(x)$
  2. $\displaystyle\lim_{x\rightarrow a} c\cdot f(x) = c\lim_{x \rightarrow a} f(x)$
  3. $\displaystyle\lim_{x \rightarrow a}[f(x)\cdot g(x)] = \left[\lim_{x\rightarrow a}f(x)\right]\cdot\left[\lim_{x\rightarrow a} g(x)\right]$
  4. $\displaystyle\lim_{x\rightarrow a} \frac{f(x)}{g(x)} = \dfrac{\lim_{x \rightarrow a} f(x)}{\lim_{x \rightarrow a}g(x)}$ if $\displaystyle\lim_{x\rightarrow a}g(x) \neq 0$.

Law 1 and 2 says you can just put the limit in front of each term.

Law 4 says you can put the limit in front of each factor.

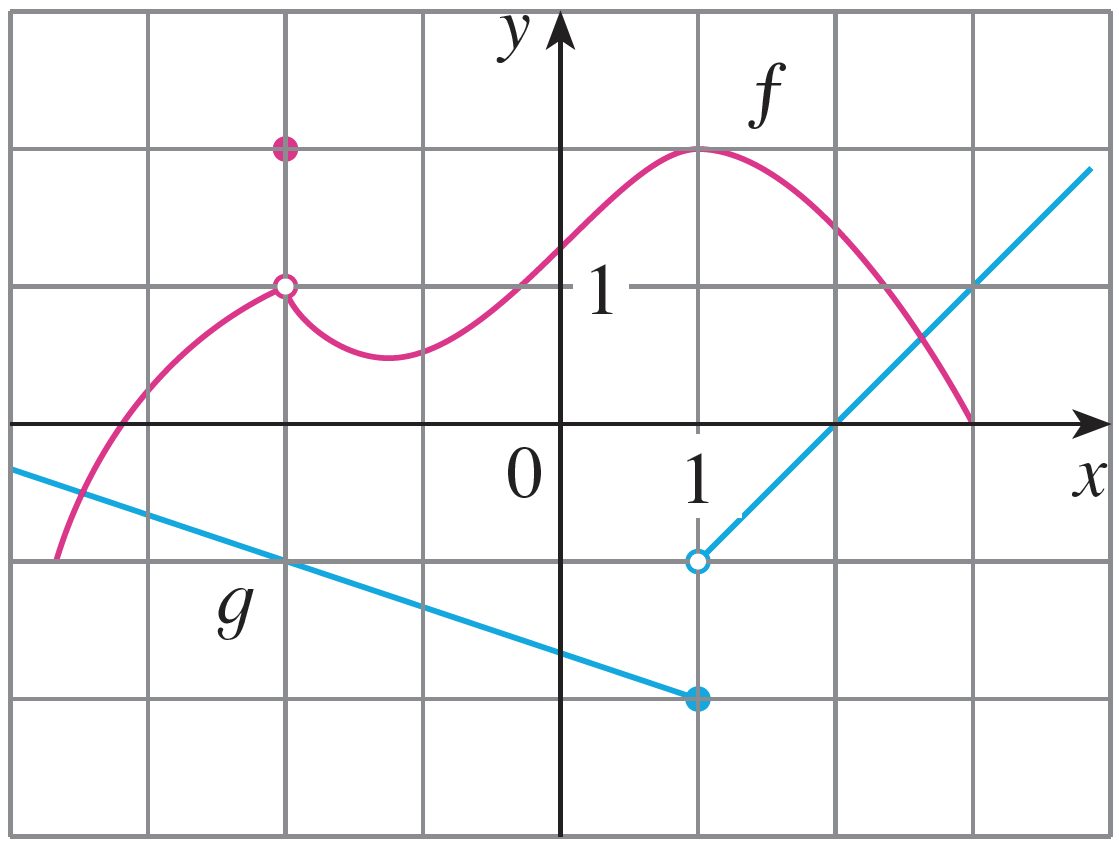Given these functions Find
  1. $\displaystyle \lim_{x \rightarrow -2} [f(x) + 5g(x)]$
  2. $\displaystyle \lim_{x \rightarrow 1} [f(x) \cdot g(x)]$
  3. $\displaystyle \lim_{x \rightarrow 2} \dfrac{f(x)}{g(x)}$

  1. From the graphs we can see \[\lim_{x \rightarrow -2} f(x) = 1 \qquad \lim_{x \rightarrow -2} g(x) = -1\] So by using the limit laws we see \begin{align}\lim_{x\rightarrow -2} [f(x) + 5g(x)] &= \lim_{x\rightarrow -2} f(x) + \lim_{x\rightarrow -2} [5g(x)] \\&= \lim_{x\rightarrow -2} f(x) + 5\lim_{x \rightarrow -2}g(x) \\&= 1 + 5\cdot (-1) = -4\end{align}
Here are six more limit laws that are extremely useful.
More Properties of Limits
Suppose $a, c \in \mathbb{R}$ and $n$ is a positive integer.
  1. $\displaystyle \lim_{x\rightarrow a}[f(x)]^n = \left[\lim_{x\rightarrow a}f(x)\right]^n$
  2. $\displaystyle\lim_{x\rightarrow a} c = c$
  3. $\displaystyle\lim_{x\rightarrow a} x = a$
  4. $\displaystyle\lim_{x\rightarrow a} x^n = a^n$
  5. $\displaystyle\lim_{x \rightarrow a}\sqrt[n]{x} = \sqrt[n]{a}$
  6. If $f(x)$ is any function, then $\displaystyle\lim_{x\rightarrow a} \sqrt[n]{f(x)}= \sqrt[n]{\lim_{x \rightarrow a} f(x)}$.
Note: this says for $n$th roots and powers of $x$, we are allowed to substitute $a$ directly. We will see why this is true in Section 1.8.
Find the following limits:
  1. $\displaystyle \lim_{x\rightarrow 5}(2x^2 - 3x + 4)$
  2. $\displaystyle \lim_{x\rightarrow -2}\dfrac{x^3 + 2x^2 - 1}{5 - 3x}$

First Look at Indeterminate Forms

Consider \[\lim_{t\rightarrow 2}\dfrac{4(t^2 -4)}{t-2}\] Let's try using the limit laws to compute this. We have \begin{align} \displaystyle\lim_{t\rightarrow 2}\dfrac{4(t^2 -4)}{t-2} &= \dfrac{\displaystyle\lim_{t\rightarrow 2} 4(t^2 - 4)}{\displaystyle\lim_{t\rightarrow 2} (t-2)} \\&= \dfrac{\displaystyle 4 (\lim_{t\rightarrow 2}t^2 - \lim_{t\rightarrow 2}4)}{\displaystyle\lim_{t\rightarrow 2} t-\lim_{t\rightarrow 2}2} \\&= \dfrac{4(2^2 - 4)}{2 - 2} \\&= \dfrac{0}{0} \end{align} The result is $0/0$, which we call an indeterminate form, which is different than dividing by zero.

Remember: we are studying limits because we need them to understand derviatives.

It turns out the calculation of the derviative is actually an indeterminate form which we will see in Chapter 2.

To deal with indeterminate forms, we employ the following strategy:

Strategy for Evaluating Indeterminate Forms
Suppose you want to evaluate $\displaystyle \lim_{x\rightarrow a}f(x)$ but end up with $0/0$. Then:
  1. Replace the original function $f(x)$ with a new function $g(x)$ that takes on the same values as the original function everywhere except at $x = a$
    In practice, this means you need to ignore the limit for now and first do some pre-calculus:
    1. Cancel out common factors.
    2. Rationalize the numerator or denominator.
    3. Simplify the expression.
    4. Potentially all of these.
  2. Then find $\displaystyle\lim_{x\rightarrow a} g(x)$ instead.
Find $\lim_{x\rightarrow 1}g(x)$ where \[g(x) = \begin{cases}x + 1 & x \neq 1 \\ \pi & x = 1\end{cases}\]
Find \[\lim_{x\rightarrow 2}\dfrac{4(x^2-4)}{x-2}\]
Find \[\lim_{h\rightarrow 0}\dfrac{\sqrt{1 + h} - 1}{h}\]
Find \[\lim_{h\rightarrow 0}\dfrac{(3+h)^2 - 9}{h}\]

Additional Properties of Limits

Recall:

\[\lim_{x\rightarrow a^+}f(x) = L = \lim_{x\rightarrow a^-}f(x) \qquad \text{if and only if} \qquad \lim_{x\rightarrow a}f(x) = L\]

Limit laws also hold for one-sided limits. This means instead of using the table technique, we can now check both left- and right-handed limits are equal with algebra!

Prove \[\lim_{x\rightarrow 0}\lvert x \rvert = 0\]
Prove \[\displaystyle\lim_{x\rightarrow 0}\dfrac{\lvert x \rvert}{x}\] does not exist.
If \[f(x) = \begin{cases} \sqrt{x - 4} & x > 4 \\ 8 - 2x & x < 4 \end{cases}\] determine if $\displaystyle \lim_{x\rightarrow 4} f(x)$ exists.

Sometimes limits can't be computed. But if we trap the function within two other functions that we know the limit of, we can find the limit of the original function itself.

The Squeeze Theorem
If $f(x) \leq g(x) \leq h(x)$ when $x$ is near $a$ (except possibly at $a$) and we know \[\lim_{x\rightarrow a}f(x) = \lim_{x\rightarrow a}h(x) = L\] then $\displaystyle \lim_{x\rightarrow a}g(x) = L$.
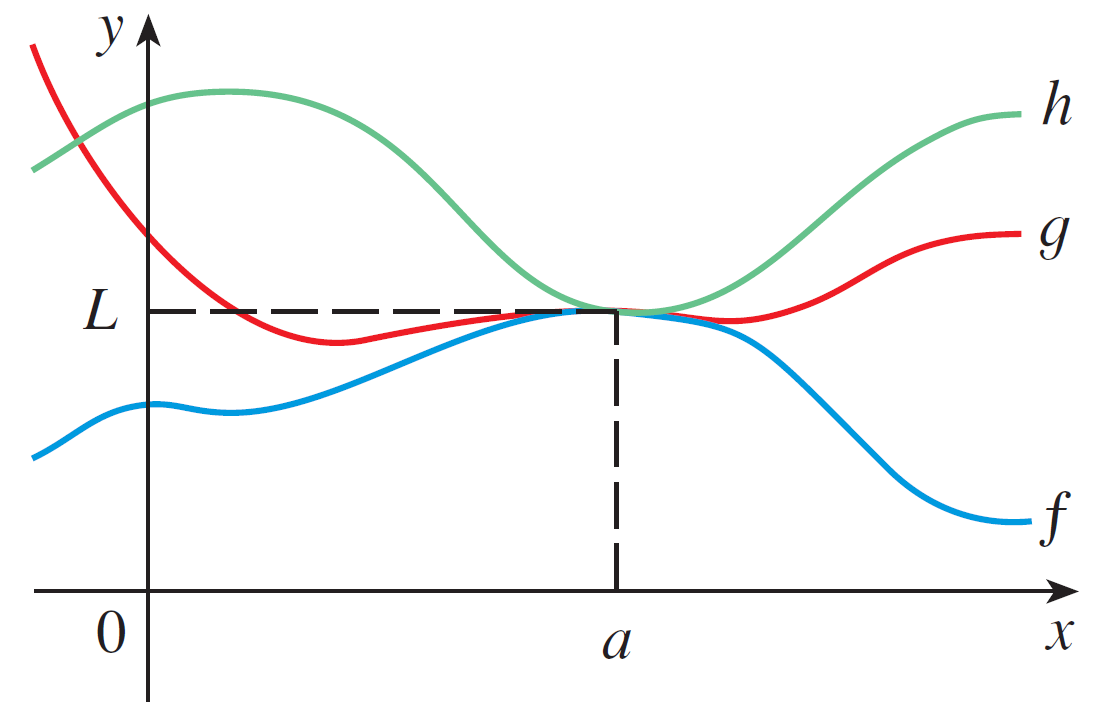
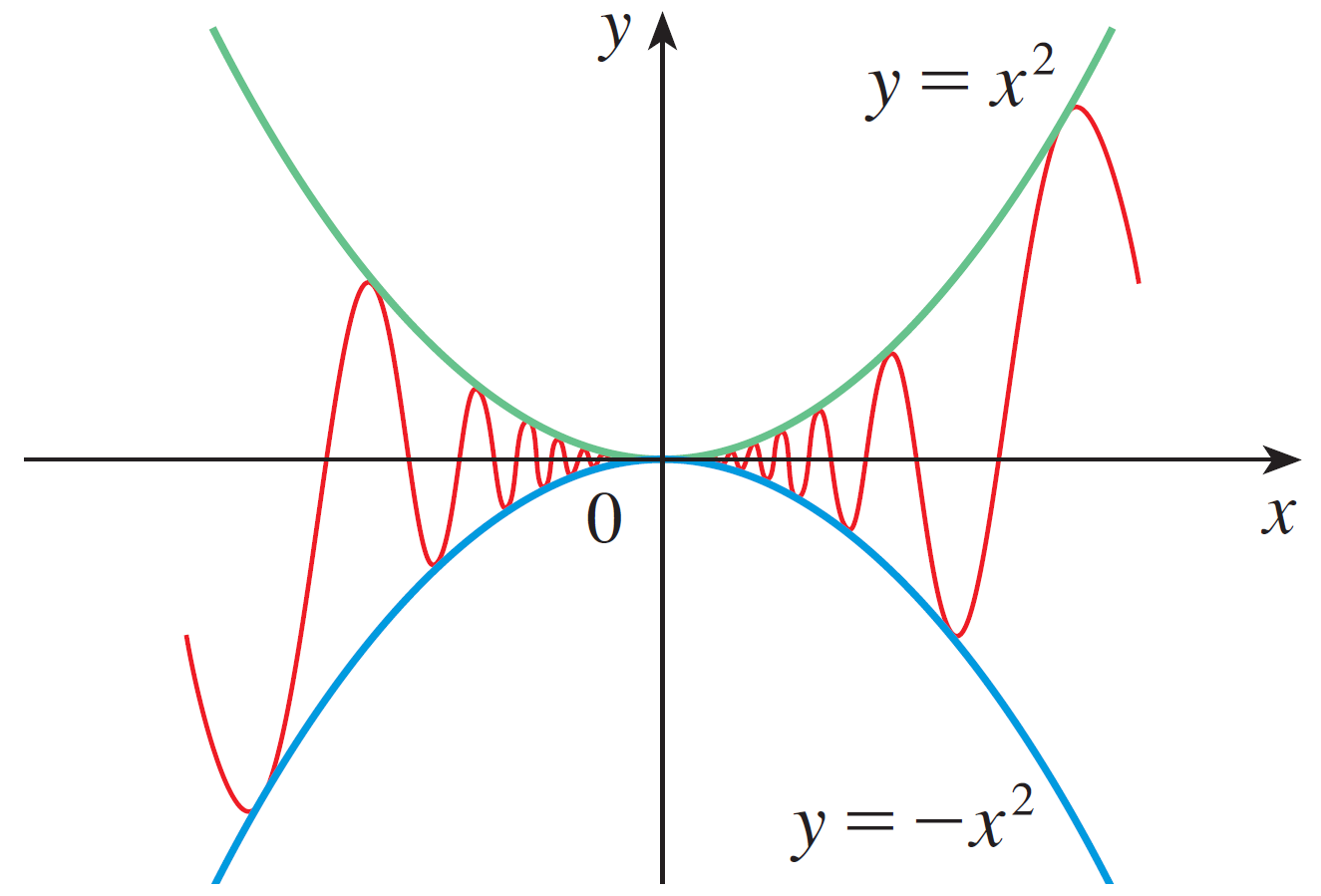
Show that $\displaystyle \lim_{x\rightarrow 0} x^2 \sin \dfrac{1}{x} = 0$.

Hint: You cannot evaluate $\lim_{x\rightarrow 0} \sin \dfrac{1}{x}$ because it does not exist: