2.3: Differentiation Formulas

It is tedious to evaluate \[f'(x) = \lim_{h\rightarrow 0} \dfrac{f(x + h) - f(x)}{h}\] every time. Let's look how we can reduce our work by looking at shortcuts.

Suppose $c, n\in \mathbb{R}$ and $f(x)$ and $g(x)$ are differentiable functions. Then
  1. $\dfrac{d}{dx} (c) = 0$
  2. $\dfrac{d}{dx} (x^n) = nx^{n-1} \ $ (called the Power Rule)
  3. $\dfrac{d}{dx} (cf(x)) = c\dfrac{d}{dx}[f(x)]$
  4. $\dfrac{d}{dx} [f(x) \pm g(x)] = \dfrac{d}{dx}[f(x)] \pm \dfrac{d}{dx}[g(x)]$

For the Power Rule, you need to make sure the derivative variable matches the variable you are applying it to.

For example \[\dfrac{d}{dx} x^2 = 2x^{2-1} = 2x\] but \[\dfrac{d}{dx}y^2 \neq 2y^{2-1}\]

For each of the following functions $f(x)$, find $f'(x)$.
  1. $f(x) = 28$
  2. $f(x) = \pi^2$
  3. $f(x) = -x$
  4. $f(x) = x^8$
  5. $f(x) = x^2\sqrt{x}$
  6. $f(x) = \sqrt{x}$
  7. $f(x) = \dfrac{1}{\sqrt[3]{x}}$
  8. $f(x) = 5x^3$
  9. $f(x) = \dfrac{3}{\sqrt{x}}$
  10. $f(x) = 4x^5 + 3x^4 - 8x^2 + x + 3$
  11. $f(t) = \dfrac{t^2}{5} + \dfrac{5}{t^3}$
The equation of motion of a particle is $s(t) = 2t^3 - 5t^2 + 3t + 4$, where $s$ is measured in centimeters and $t$ in seconds. Find acceleration as a function of time and compute the acceleration after 2 seconds.

Product and Quotient Rules

We know how to take derivatives of sums, constants, and $x^n$. What about products?

Product Rule
\[\dfrac{d}{dx}[f(x)g(x)] = f(x)g'(x) + g(x)f'(x)\]
Find the derivatives of the following:
  1. $f(v) = (v^2 +1)(v^2 - 1)$
  2. $f(x) = x^3(\sqrt{x} + 1)$

How about quotients?

Quotient Rule
\[\dfrac{d}{dx}\left[\dfrac{f(x)}{g(x)}\right] = \dfrac{g(x)f'(x) - f(x)g'(x)}{[g(x)]^2}\]

You can remember this by thinking "low Dhigh minus high Dlow, square the bottom, away you go."

Differentiate (find the derivative) of the following:
  1. $f(x) = \dfrac{x^2 + x - 2}{x^3 + 6}$

The tangent line has a point of tangency. If you take the line that is perpendicular to the tangent line at the point of tangency, this is called the normal line.

Here is an illustration: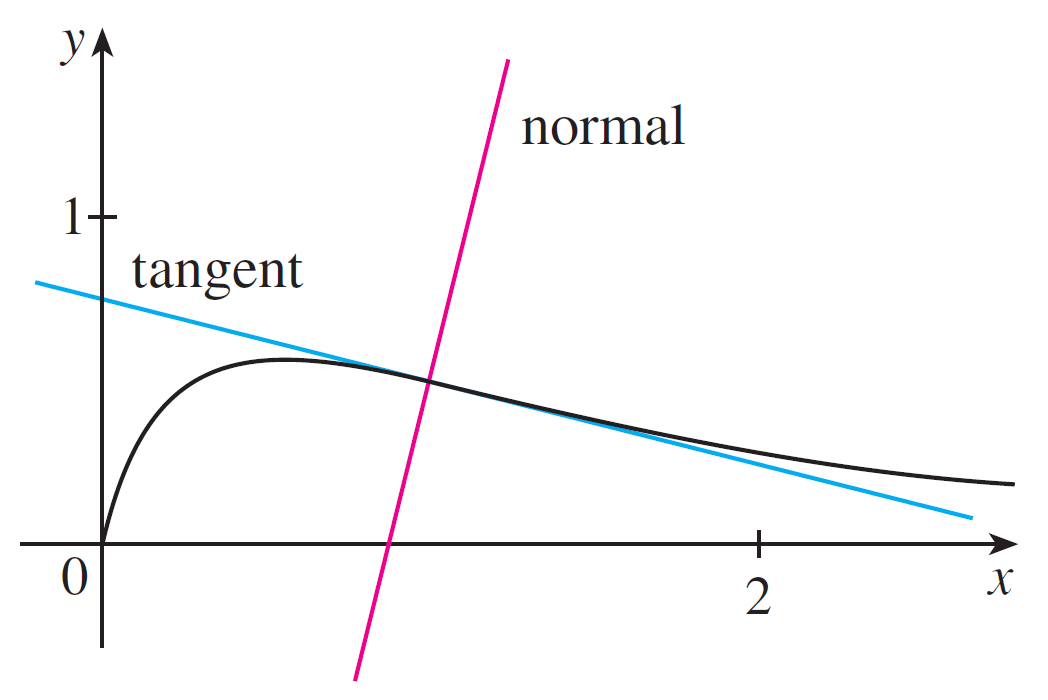

Find equations of the tangent line and normal line to the function $y = \dfrac{\sqrt{x}}{1 + x^2}$ at the point $\left(1, \frac{1}{2}\right)$.