4.2: The Definite Integral

The "area underneath the curve" is a limit of adding up smaller and smaller rectangles.

This limit is called the definite integral:

The definite integral of $f(x)$ from $a$ to $b$ is \[\int^b_a f(x) \ dx = \lim_{n\rightarrow \infty} \sum^n_{i=1} f(x_i)\Delta x\] where

$\Delta x$ is the width of one rectangle, or $\Delta x = \dfrac{b - a}{n}$
$x_i$ is the right endpoint of the $i$th rectangle, where $x_i = a + i\cdot\Delta x$

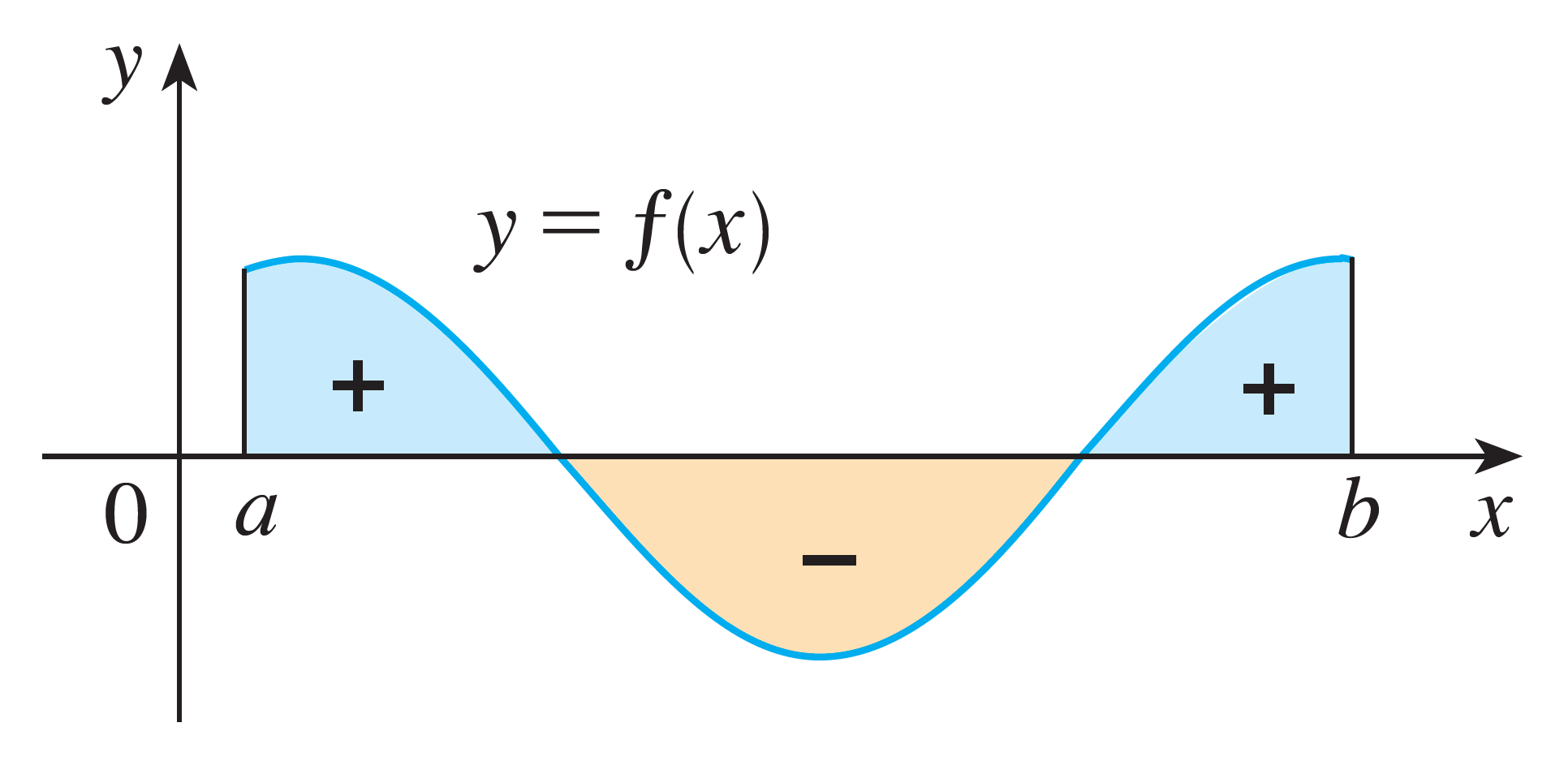
By convention, if $f(x)$ is above the $x$-axis, the area underneath the curve is positive. If $f(x)$ is under the $x$-axis, the area is negative.

When dealing with integrals, you need to treat the expression \[\int^b_a f(x) \ dx\] as one entire entity; you cannot pull out the $dx$ or manipulate the expressions to the right of the integral.

Integrals are hard to evaluate.

For example, we saw that the area underneath the curve of $f(x) = x^2$ on $[0, 1]$ is the following calculation: \[\int^b_a x^2 \ dx = \lim_{n\rightarrow \infty}\dfrac{1}{n^3}\sum^n_{i = 1}i^2\]

But sometimes you can use geometric arguments to evaluate integrals.

Evaluate the integral $\displaystyle \int^1_0 \sqrt{1 - x^2} \ dx$.

Evaluate the integral $\displaystyle \int^3_0 x - 1 \ dx$.

Properties of the Definite Integral

Because the definite integral is an area, you can manipulate integrals with geometric intuition:

Suppose $c \in \mathbb{R}$. Then:

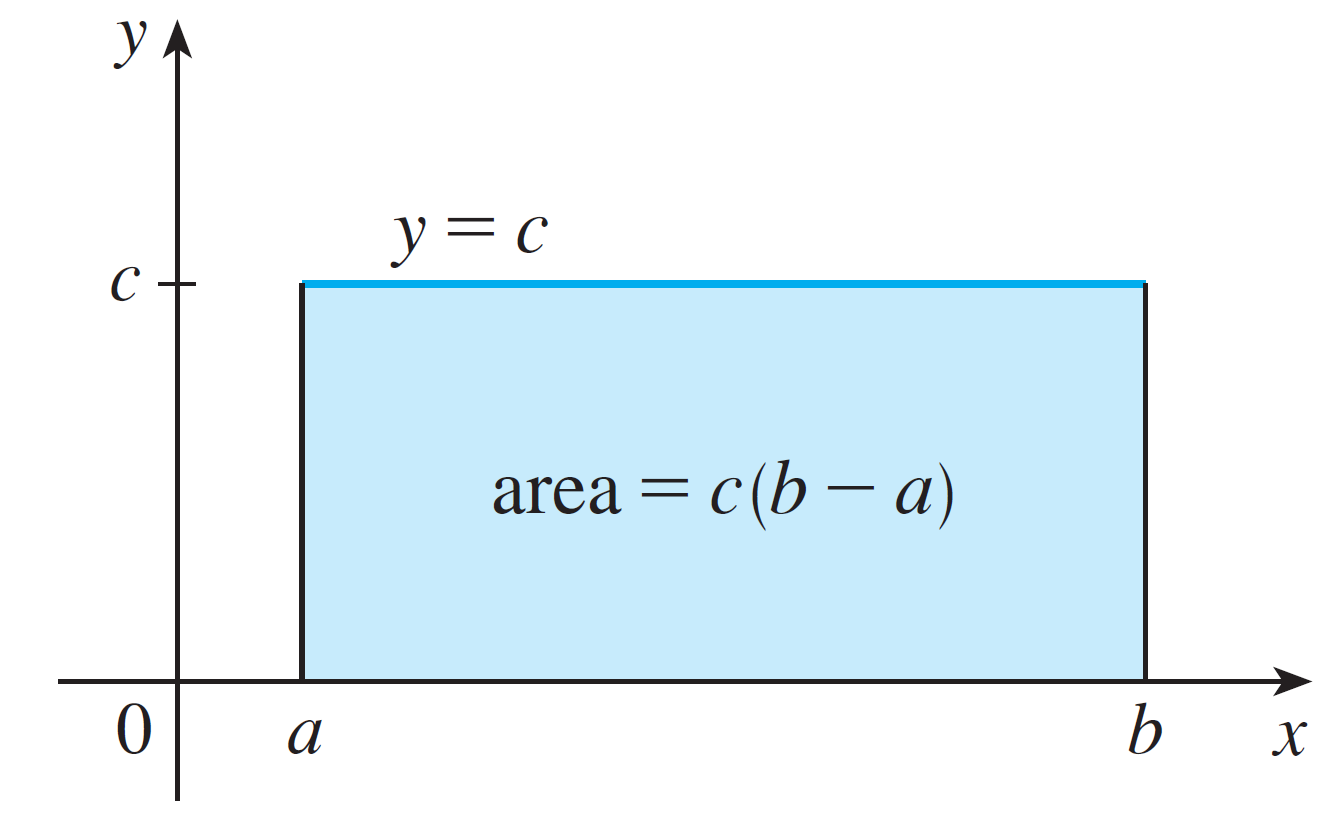
$\displaystyle \int^b_a c \ dx = c \cdot (b - a)$
$\displaystyle \int^b_a [f(x) \pm g(x)]\ dx = \int^b_a f(x) \ dx \pm \int^b_a g(x) \ dx$
$\displaystyle \int^b_a cf(x) \ dx = c\int^b_a f(x) \ dx$
$\displaystyle \int^c_a f(x) \ dx + \int^b_c f(x) \ dx = \int^b_a f(x) \ dx$
$\displaystyle \int^a_a f(x) \ dx = 0$
$\displaystyle \int^a_b f(x) \ dx = -\int^b_a f(x) \ dx$

Evaluate the integral $\displaystyle \int^3_3 \sin^2(x)\cos^2(x)(x^9 - x^2 + 1) \ dx$.

If $\displaystyle \int^{10}_0 f(x) \ dx = 17$ and $\displaystyle \int^8_0 f(x) \ dx = 12$, find $\displaystyle \int^{10}_8 f(x) \ dx$.

Evaluate $\displaystyle \int^1_0 1 + 4x^2 \ dx$.