Functions Crash Course for Calculus

Goals:

Describe the object we are going to use calculus on and how it appears in our everyday lives.
Learn how to mathematically represent a function and manipulate them while avoiding common mistakes.

Functions All Around Us

The word function describes a dependence of one quantity on another. For example:

The current room temperature is a function of time.
After a flight takes off, the total distance a plane travels is a function of time since takeoff.

Functions should be thought of as a machine.

For example, when you input time, you get out the current temperature. Any temperature app you have uses this idea.

Notice that at a single time point, only one output is returned. This leads us to the mathematical definition of a function.

A function $f$ is a rule that assigns to each element $x$ in a set $A$ to exactly one element, called $f(x)$ in a set $B$.

What are some examples of functions you can think of?

Evaluating a Function

A simple way to mathematically represent input-output is with the notation $f(x)$.

Here, the $x$ between the parenthesis is your input variable, and $f(x)$ is your output.

A function is defined by the formula \[f(x) = x^2 - 2\] Evaluate the following:

$f(0)$
$f(-1)$
$f(-a)$
$f(x + h)$
$f(x + h) - f(x)$

Beware: everything between the parenthesis must be treated as input.

From now on, when instructed to perform something, like "evaluate $f(x + h)$" you must fully simplify.

For example, this can mean:

expand then combine like terms whenever you can
use Fraction Law 5 to cancel factors if applicable
multiply all fractional expressions together to write your answer as one fraction
etc.

A function is defined by \[g(x) = x^2 - x\] Evaluate the following:

$g(0)$
$g(-1)$
$g(-a)$
$g(x + h)$
$g(x + h) - g(x)$

Domain of a Function

The domain of a function is the set of all inputs you can input to get out a valid real number.

For the function $f(x) = \dfrac{1}{x}$, which of the following numbers are in the domain?

$-2$
$-1$
$0$
$\frac{1}{2}$
$2$

When finding domain, follow two steps:

Look for problems. These are numbers, when evaluated, result in something that is not a real number. Problems are

Plugging a number where you end up dividing by zero.
Plugging a number where you end up taking the square root of a negative number.

Remove the problems from $\mathbb{R}$ and write your answer in interval notation.

What is the domain of $f(x) = \dfrac{1}{x}$?

What is the domain of $f(x) = \sqrt{x - 1}$?

What is the domain of $g(x) = \dfrac{1}{x^2 - x}$?

Piecewise Functions

The rest of this lecture has been recorded, available at this YouTube link.

Piecewise functions are functions where you have multiple different functions on different parts of the domain.

For example, \[f(x) = \begin{cases} x^2 & x \leq 1 \\ -2x + 3 & x > 1\end{cases}\] is a piecewise function.

Here's how to read this: If your input $x$ is less than or equal to 1, then you need to plug it into $x^2$.

If your input $x$ is strictly greater than 1, plug it into $-2x + 3$.

For the above function, evaluate $f(0), f(1)$ and $f(2)$.

The Coordinate Plane

A point in space can be described by starting at a point, then moving to it.

Plot the points $(1,1), (-2, -3), (-3, 2)$ and $(4, 2)$ in the coordinate plane.

Graph of a Function

You can describe a function like \[f(x) = x^2 + 2\] in four different ways.

In English: Square the input and add two
Algebraically: $x^2 + 2$
With a table of values
With a graph in the coordinate plane

The graph of a function $f(x)$ with domain $A$ is formally defined as a set of coordinates \[\{(x, f(x)) : x \in A\}\]

The graph is especially important because you can quickly spot visual patterns in certain types of functions.

It also gives us an intuitive understanding of calculus concepts instead of just looking at a bunch of messy algebra like \[f(x) = \sin(x)\tan(x)e^{4x}(x^4 - x^2)\]

What is the geometric intution behind the symbol $f(x)$?

Graph the piecewise function \[f(x) = \begin{cases} x^2 & x \leq 1 \\ 2x - 3 & x > 1\end{cases}\] by hand.

Graph the function $y = \lvert x \rvert$.

The graph helps us determine if a curve in the plane is actually a function.

Vertical Line Test
A curve in the $xy$-plane is the graph of a function of $x$ if and only if no vertical line intersects the curve more than once.

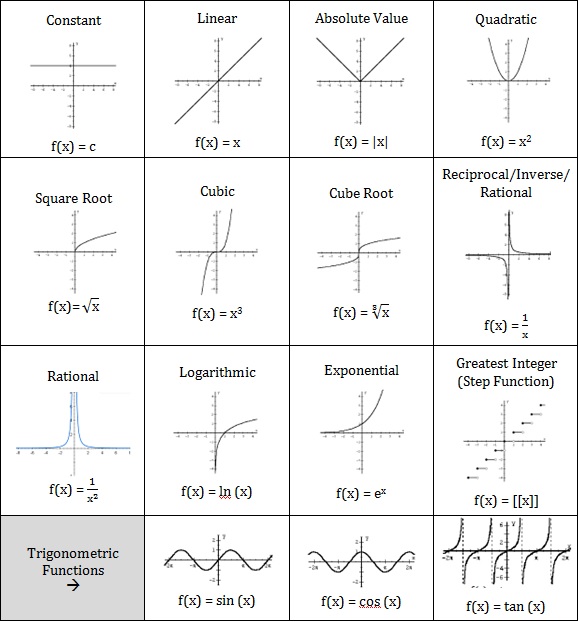
Base Functions to be Familiar With

In calculus, you need to be familiar with what we call "parent functions:" linear, absolute value, polynomial, rational and trigonometric functions.

These are all part of the prerequisite of MATH 141.

Here are good resources if you need a refresher of these types. I recommend the textbook Precalculus, Mathematics for Calculus by James Stewart, 7th Edition.

For polynomials: pages 246-256 in Precalculus
For rationals: Section 3.6 in Precalculus (pages 295-307)
For trigonometric functions:
- Interactive lecture notes on Section 5.1 describing the unit circle
- Interactive lecture notes on Section 5.2 describing trigonometric functions with animations on how they are created from the unit circle.
- Section 5.1 and 5.2 in Precalculus

Moreover, Section 1.2 in our Calculus textbook contains a very terse summary of all of these function types. If you do not remember the details of the function $\tan(x)$, for example, I recommend the above list as another reference.

Here's a visual guide to a few parent functions we'll encounter.

Holes

When you cancel a common factor in a rational function, you must exclude the zero of that factor from the domain.

Such a factor is called a hole.

Redefine the rational function $f(x) = \dfrac{x^2 + 2x + 1}{x+1}$ with the domain exclusion.

Redefine the rational function $f(x) = \dfrac{x^3 - x}{x}$ with the domain exclusion.

Creating New Functions with Operations

$+, -, \times, \div$ functions together is done by performing the specified operation on the function output. Let's look at some examples.

Be careful when you are subtracting and multiplying functions together. If you are multiplying by $\geq 2$ terms, do not forget parenthesis.

Let $f(x) = x^2 + x$ and $g(x) = -x^2 - x$. Find the following:

$f(x)+g(x), f(x)-g(x), f(x)g(x), \frac{f}{g}$ and their domains
$\frac{f(0)}{g(0)}$

Let's first find the domains and intersect them. Both functions have domain $\mathbb{R}$. Following the above table, we see that \begin{align} (f+g)(x) &= f(x) + g(x) &&= x^2 + x + -x^2 - x = 0 \\ (f-g)(x) &= f(x) - g(x) &&= x^2 + x - (-x^2 - x) = x^2 + x + x^2 + x = 2x^2 + 2x \\ (f\cdot g)(x) &= f(x)\cdot g(x) &&= (x^2 + x)(-x^2 - x) = (x^2 + x)(-x^2) + (x^2 + x)(-x) = -x^4 - x^3 - x^3 - x^2 = -x^4 - 2x^3 - x^2 \\ \left(\frac{f}{g}\right)(x) &= \frac{f(x)}{g(x)} &&= \frac{x^2 + x}{-x^2 -x} = \frac{x(x+1)}{-x(x + 1)} = \frac{1}{-1} = -1 , \ x \neq 0, x \neq -1 \\ \end{align}
We have \[\dfrac{f(0)}{g(0)} = \dfrac{0^2 + 0}{-0^2 - 0} = \dfrac{0}{0}\] which is undefined.

Adding functions together has a nice graphical interpretation. In this example, we see the graph $f(x) + g(x)$ is just the vertical heights of $f(x)$ and $g(x)$ added together.

Function Composition

Function evaluation on a number is straightforward: the preceding example utilized this concept. What if we evaluate a function on another function? This idea is called function composition.

Given two functions $f$ and $g$, the composite function $f \circ g$ (also called the composition of $f$ and $g$) is defined by \[(f\circ g)(x) = f(g(x))\]

To evaluate a function composition, you first plug in $g(x)$ into $f(x)$, and wherever there is an $x$ in $f(x)$, substitute the definition of $g(x)$ there.

Suppose $f(x) = x^2$ and $g(x) = x-3$. Find the functions $f\circ g$ and $g \circ f$

We see that \[(f\circ g)(x) = f(g(x)) = f(x-3) = (x-3)^2\] and \[(g\circ f)(x) = g(f(x)) = g(x^2) = x^2 - 3\]$.

Ideas:

This shows that the operation $\circ$ is not commutative, i.e. $f\circ g \neq g \circ f$. Do not mistake $f\circ g$ to mean function multiplication!
We can also take compositions of three or more functions. For example, $f\circ g \circ h = f(g(h(x)))$.

Find $f\circ g \circ h$ where $f(x) = \frac{x}{x+1}, g(x) = x^{10}, h(x) = x+3$.

\begin{align} (f\circ g \circ h)(x) &= f(g(h(x)))\\ &= f(g(x+3))\\ &= f((x+3)^{10})\\ &= \frac{(x+3)^{10}}{(x+3)^{10}+1} \end{align}

The concept in these last three composition examples will be used extensively in calculus.

Given $F(x) = \sqrt[4]{x + 9}$, find functions $f$ and $g$ such that $F = f\circ g$.

We can think of this function as the $\sqrt[4]{\cdot}$ as the outside function, and $x + 9$ as the inside function.
Since $f\circ g$ is the desired composition, let $g(x) = x+9$ and $f(x) = \sqrt[4]{x}$. Then \[(f\circ g)(x) = f(g(x)) = f(x+9) = \sqrt[4]{x+9} = F(x)\]

Suppose $F(x) = \sin^3(x)$. Find functions $f$ and $g$ where $F = f \circ g$.

Suppose $F(x) = \sin(x^3)$. Find functions $f$ and $g$ where $F = f \circ g$.