3.4: Limits of Functions at Infinity

A major concept in calculus is integration. To understand what the integral is, we discuss four different ideas:

  1. Limits at infinity, or $\lim_{x\rightarrow \infty}f(x)$
  2. Mean Value Theorem
  3. Antiderivatives
  4. The integral itself

In Section 1.5 we looked at when a limit is infinity (vertical asymptotes).

We now look at a limit at infinity, or when the limiting variable increases or decreases without bound.

Definition of a Limit at Infinity

The function $f$ has the limit $L$ as $x$ increases without bound (meaning $x\rightarrow \infty$), written as \[\lim_{x\rightarrow \infty}f(x) = L\] if $f(x)$ can be made arbitrarily close to $L$ by taking $x$ large enough.

Similarly, the function $f$ has the limit $M$ as $x$ decreases without bound (meaning $x\rightarrow -\infty$), written as \[\lim_{x\rightarrow -\infty}f(x) = M\] if $f(x)$ can be made arbitrarily close to $M$ by taking $x$ to be a sufficiently large negative number.

If $L$ or $M$ from above exist, then $f(x)$ has a horizontal asymptote.

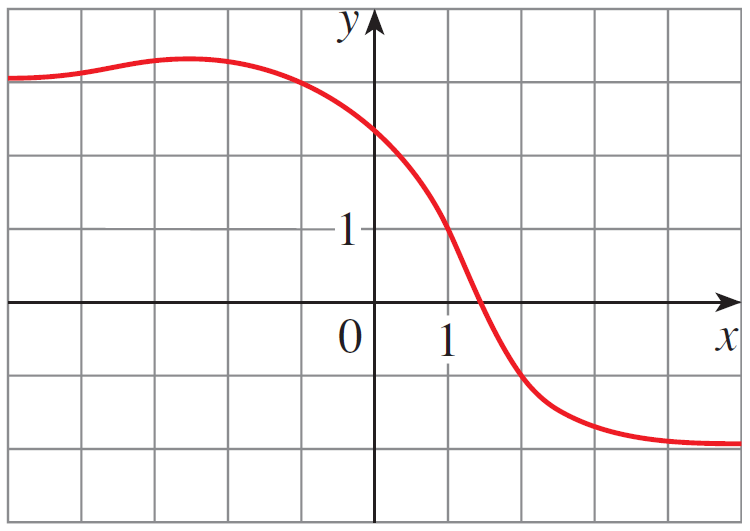Given this function $f(x)$ find $\displaystyle\lim_{x\rightarrow \infty} f(x)$ and $\displaystyle\lim_{x\rightarrow -\infty} f(x)$
Find these limits: \[\lim_{x\rightarrow \infty} \dfrac{1}{x} \qquad \lim_{x\rightarrow -\infty} \dfrac{1}{x}\]
For all $n > 0$, we have \[\lim_{x\rightarrow \infty} \dfrac{1}{x^n} = 0 \qquad \text{and} \qquad \lim_{x\rightarrow-\infty}\dfrac{1}{x^n} = 0\] if $\frac{1}{x^n}$ is defined.

You can quickly verify this because there exist horizontal asymptotes for any value of $n$.

Limit laws also hold for limits at infinity. For example: \[\lim_{x\rightarrow\infty}[f(x) + g(x)] = \lim_{x\rightarrow\infty}f(x) + \lim_{x\rightarrow\infty}g(x)\]

Find the following limits:
  1. $\displaystyle\lim_{t\rightarrow \infty}\dfrac{8t}{1 + 4t^2}$
  2. $\displaystyle\lim_{x\rightarrow\infty}\left(\sqrt{x^2 + 1} - x\right)$
  3. $\displaystyle\lim_{x\rightarrow\infty}\sin x$
  4. $\displaystyle\lim_{x\rightarrow \infty} \sin \dfrac{1}{x}$
  5. $\displaystyle\lim_{x\rightarrow \infty} \dfrac{\sqrt{2x^2 + 1}}{3x - 5}$
    The largest power term of $x$ in the denominator is $x$. Because $x\rightarrow \infty$, $x$ is growing without bound, so $x$ must be positive. Recalling that \[\sqrt{x}\cdot \dfrac{1}{x} = \sqrt{x}\cdot\sqrt{\dfrac{1}{x^2}} = \sqrt{x\cdot \dfrac{1}{x^2}}\] by the Laws of Exponents #4, we use this move in the numerator: \begin{align} \lim_{x\rightarrow \infty} \dfrac{\sqrt{2x^2 + 1}}{3x - 5} &= \lim_{x\rightarrow \infty} \dfrac{\dfrac{\sqrt{2x^2 + 1}}{x}}{\dfrac{3x - 5}{x}} \\&= \lim_{x\rightarrow \infty} \dfrac{\sqrt{\dfrac{2x^2 + 1}{x^2}}}{3 - \dfrac{5}{x}} \\&= \dfrac{\displaystyle \lim_{x\rightarrow \infty} \sqrt{2 + \dfrac{1}{x^2}}}{\displaystyle \lim_{x\rightarrow \infty} \left(3 - \dfrac{5}{x}\right)} \\&= \dfrac{\sqrt{\displaystyle \lim_{x\rightarrow \infty} 2 + \lim_{x\rightarrow\infty} \dfrac{1}{x^2}}}{\displaystyle \lim_{x\rightarrow \infty} 3 - 5\lim_{x\rightarrow \infty} \dfrac{1}{x}} \\&= \dfrac{\sqrt{2 + 0}}{3 - 5 \cdot 0} \\&= \dfrac{\sqrt{2}}{3} \end{align}

Infinite Limits at Infinity

The notation $\lim_{x\rightarrow\infty}f(x) = \infty$ means the values of $f(x)$ become large as $x$ becomes large.

Note that $\infty$ is not a number; it is used to represent a specific characteristic about $f(x)$.

Find the following limits:
  1. $\displaystyle\lim_{x\rightarrow\infty}x^3$
  2. $\displaystyle\lim_{x\rightarrow-\infty}x^3$
  3. $\displaystyle\lim_{x\rightarrow\infty}(x^2 - x)$
  4. $\displaystyle\lim_{x\rightarrow\infty}\dfrac{x^2 + x}{3 - x}$